Common Denominator For 3 And 4
Juapaving
Apr 01, 2025 · 5 min read
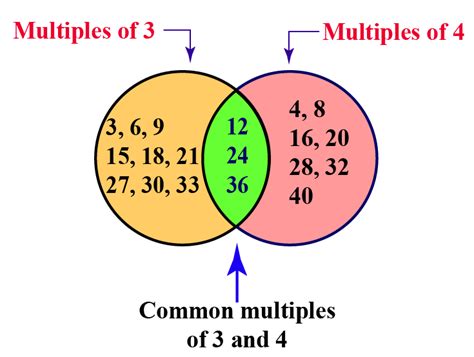
Table of Contents
Finding the Common Denominator for 3 and 4: A Deep Dive into Fractions
Finding a common denominator is a fundamental skill in mathematics, essential for adding, subtracting, comparing, and simplifying fractions. While seemingly simple for small numbers like 3 and 4, understanding the underlying principles unlocks a deeper appreciation for working with fractions and lays the groundwork for more complex mathematical concepts. This article delves into the intricacies of finding the common denominator for 3 and 4, exploring various methods, explaining the reasoning behind each, and providing practical examples to solidify your understanding.
Understanding Fractions and Denominators
Before we dive into finding the common denominator, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator is 2 (we have two parts), and the denominator is 3 (the whole is divided into three equal parts). The denominator defines the size of each part; a larger denominator means smaller parts.
When adding, subtracting, or comparing fractions, they must share the same denominator. This common denominator provides a consistent unit of measurement, allowing for accurate calculations.
Methods for Finding the Common Denominator for 3 and 4
There are several ways to find a common denominator for 3 and 4. Let's explore the most common methods:
1. Listing Multiples
This is a straightforward method, particularly helpful for smaller numbers. We simply list the multiples of each denominator until we find a common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
Notice that 12 and 24 appear in both lists. Therefore, 12 and 24 are common multiples of 3 and 4. In this context, they are also referred to as common denominators. We typically choose the least common multiple (LCM), which is the smallest common multiple. In this case, the LCM of 3 and 4 is 12.
2. Prime Factorization
Prime factorization is a more systematic approach, especially useful for larger numbers. It involves breaking down each denominator into its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 4: 2 x 2 (2 is a prime number)
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
Multiply these highest powers together: 4 x 3 = 12. Therefore, the LCM, and thus the least common denominator, is 12.
3. Using the Formula: LCM(a, b) = (a x b) / GCD(a, b)
This method uses the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
- Finding the GCD of 3 and 4: The GCD of 3 and 4 is 1 (as 1 is the only common divisor).
Now, we apply the formula:
LCM(3, 4) = (3 x 4) / GCD(3, 4) = 12 / 1 = 12
This formula provides a more efficient calculation for larger numbers, although understanding prime factorization is still beneficial for grasping the underlying concept.
Converting Fractions to a Common Denominator
Once we've found the common denominator (12), we can convert the fractions 1/3 and 1/4 to equivalent fractions with this denominator.
-
Converting 1/3 to a denominator of 12: We multiply both the numerator and denominator by 4 (because 12/3 = 4): (1 x 4) / (3 x 4) = 4/12
-
Converting 1/4 to a denominator of 12: We multiply both the numerator and denominator by 3 (because 12/4 = 3): (1 x 3) / (4 x 3) = 3/12
Now we have equivalent fractions: 4/12 and 3/12. These fractions represent the same proportions as 1/3 and 1/4, but with a common denominator, allowing us to easily perform addition, subtraction, and comparison.
Applications of Finding Common Denominators
The ability to find a common denominator is vital in numerous mathematical operations and real-world applications:
-
Adding and Subtracting Fractions: This is the most common application. Without a common denominator, we cannot directly add or subtract fractions. For example: 1/3 + 1/4 = 4/12 + 3/12 = 7/12
-
Comparing Fractions: Determining which fraction is larger or smaller requires a common denominator. For instance, comparing 1/3 and 1/4 becomes easy once they are expressed as 4/12 and 3/12, respectively. Clearly, 4/12 > 3/12, meaning 1/3 > 1/4.
-
Solving Equations: Many algebraic equations involve fractions, and finding a common denominator is often crucial for simplifying and solving these equations.
-
Real-world applications: From baking (measuring ingredients) to construction (calculating measurements), common denominators are used in various practical situations requiring precise calculations with fractional quantities.
Advanced Concepts and Extensions
The concept of common denominators extends beyond simple fractions:
-
Algebraic Fractions: The same principles apply when dealing with fractions containing variables (algebraic fractions). Finding a common denominator remains essential for adding, subtracting, and simplifying these expressions.
-
Rational Expressions: Rational expressions are algebraic fractions, and manipulating them effectively relies heavily on finding common denominators.
-
Complex Fractions: Complex fractions involve fractions within fractions. Simplifying complex fractions often requires finding common denominators at multiple levels.
Conclusion: Mastering the Common Denominator
Finding a common denominator for 3 and 4, while seemingly elementary, serves as a gateway to a deeper understanding of fractions and their significance in mathematics. Mastering this fundamental concept empowers you to tackle more complex fractional calculations, opens doors to advanced mathematical concepts, and equips you with the practical skills needed for countless real-world applications. Whether you choose the method of listing multiples, prime factorization, or the LCM formula, the key lies in understanding the underlying principles and selecting the most efficient approach based on the numbers involved. The consistent application of these methods strengthens your mathematical foundation and builds confidence in your problem-solving abilities. Remember, practice is key to mastering this essential skill. Regularly working with fractions and applying these methods will solidify your understanding and make finding common denominators a simple and intuitive task.
Latest Posts
Latest Posts
-
Are Angiosperms Gametophyte Or Sporophyte Dominant
Apr 02, 2025
-
How Many Centimeters Are In 14 Inches
Apr 02, 2025
-
5 Letter Words End In On
Apr 02, 2025
-
List The Following Events In The Correct Order
Apr 02, 2025
-
How Tall Is 33 Inches In Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Common Denominator For 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
