How Many Solutions Does This Equation Have
Juapaving
Apr 01, 2025 · 5 min read
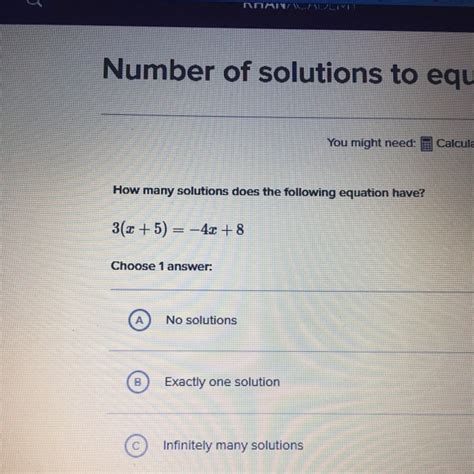
Table of Contents
How Many Solutions Does This Equation Have? A Deep Dive into Solving Equations
Determining the number of solutions an equation possesses is a fundamental concept in mathematics, impacting various fields from physics and engineering to computer science and economics. The approach to finding the number of solutions depends heavily on the type of equation: linear, quadratic, polynomial, trigonometric, exponential, or logarithmic, each presenting unique characteristics and solution methods. This article explores various equation types, demonstrating techniques to determine the number of solutions and providing examples to solidify understanding.
Understanding the Concept of Solutions
Before diving into different equation types, let's clarify what we mean by "solutions." A solution to an equation is a value (or set of values) that, when substituted into the equation, makes the equation true. For instance, in the equation x + 2 = 5, the solution is x = 3 because substituting 3 for x results in a true statement (3 + 2 = 5). Equations can have one solution, multiple solutions, or no solutions at all.
Linear Equations: A Single Solution
Linear equations are equations of the form ax + b = 0, where 'a' and 'b' are constants and 'a' is not zero. These equations always have exactly one solution. The solution can be found by isolating the variable 'x':
x = -b/a
Example:
2x + 6 = 0
Subtracting 6 from both sides:
2x = -6
Dividing both sides by 2:
x = -3
Therefore, the linear equation 2x + 6 = 0 has only one solution, x = -3.
Quadratic Equations: Up to Two Solutions
Quadratic equations are equations of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants and 'a' is not zero. These equations can have zero, one, or two real solutions. The number of solutions is determined by the discriminant, denoted as Δ (Delta):
Δ = b² - 4ac
- Δ > 0: Two distinct real solutions
- Δ = 0: One real solution (a repeated root)
- Δ < 0: No real solutions (two complex solutions)
Examples:
- x² - 4x + 3 = 0
Here, a = 1, b = -4, c = 3. The discriminant is:
Δ = (-4)² - 4(1)(3) = 16 - 12 = 4 > 0
Since Δ > 0, this equation has two distinct real solutions. These can be found using the quadratic formula or factoring.
- x² - 6x + 9 = 0
Here, a = 1, b = -6, c = 9. The discriminant is:
Δ = (-6)² - 4(1)(9) = 36 - 36 = 0
Since Δ = 0, this equation has one real solution (a repeated root).
- x² + 2x + 5 = 0
Here, a = 1, b = 2, c = 5. The discriminant is:
Δ = (2)² - 4(1)(5) = 4 - 20 = -16 < 0
Since Δ < 0, this equation has no real solutions (two complex solutions involving the imaginary unit 'i').
Polynomial Equations: Variable Number of Solutions
Polynomial equations are equations of the form aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀ = 0, where 'aₙ', 'aₙ₋₁', ..., 'a₁', 'a₀' are constants and 'aₙ' is not zero. The degree of the polynomial (the highest power of x) determines the maximum number of solutions. A polynomial of degree 'n' can have at most n real solutions. However, it's crucial to remember that some solutions may be repeated, and some may be complex. Finding the exact number of real solutions for higher-degree polynomials can be challenging and often requires numerical methods.
Example:
A cubic polynomial (degree 3) can have three, two, or one real solution, depending on its coefficients. It might also have complex solutions.
Trigonometric Equations: Infinitely Many Solutions (Typically)
Trigonometric equations involve trigonometric functions like sine, cosine, and tangent. These equations often have infinitely many solutions due to the periodic nature of trigonometric functions. Solutions are typically found within a specific interval (e.g., 0 to 2π) and then generalized to encompass all possible solutions using the periodicity of the functions.
Example:
sin(x) = 1/2
The principal solution is x = π/6. However, since the sine function has a period of 2π, the general solution is given by:
x = π/6 + 2kπ and x = 5π/6 + 2kπ, where k is an integer.
Exponential and Logarithmic Equations: Typically One Solution
Exponential equations involve variables in the exponent, such as 2ˣ = 8. Logarithmic equations involve logarithms, such as log₂(x) = 3. These types of equations usually have one solution, although there might be cases with no solutions or extraneous solutions that need to be excluded.
Example:
2ˣ = 8
Taking the logarithm base 2 of both sides:
x = log₂(8) = 3
Thus, the equation has one solution, x = 3.
Systems of Equations: Multiple Solutions Possible
When dealing with a system of equations (two or more equations with multiple variables), the number of solutions depends on the nature of the equations. The system can have:
- One unique solution: The lines (or planes) intersect at one point.
- Infinitely many solutions: The lines (or planes) coincide.
- No solutions: The lines (or planes) are parallel and do not intersect.
Techniques for Determining the Number of Solutions
Several techniques help determine the number of solutions an equation has:
- Graphical analysis: Plotting the equation can visually reveal the number of intersections with the x-axis (representing the number of real solutions).
- Algebraic manipulation: Using algebraic techniques like factoring, the quadratic formula, or completing the square can lead to explicit solutions or reveal the nature of the solutions (real or complex).
- Discriminant analysis (for quadratic equations): Calculating the discriminant helps determine the number of real solutions.
- Numerical methods: For complex equations, numerical methods like Newton-Raphson can approximate the solutions and provide insights into their number.
Conclusion: A Versatile Field
Determining the number of solutions an equation has is a crucial skill in mathematics. The approach varies widely depending on the type of equation. Understanding the underlying principles and applying appropriate techniques ensures accurate solutions and a deeper grasp of mathematical relationships. Remember to always consider the context of the problem and the possibility of extraneous solutions when interpreting results. The journey through different equation types reveals the richness and complexity of mathematics, showcasing the beauty of its systematic approaches to solving problems.
Latest Posts
Latest Posts
-
40 C By 70cm Kite Area
Apr 02, 2025
-
Is Denatured Alcohol And Rubbing Alcohol The Same
Apr 02, 2025
-
Do Prokaryotic Cells Have Membrane Bound Organelles
Apr 02, 2025
-
Common Multiples Of 4 And 5
Apr 02, 2025
-
How Many Cubic Inches In A Foot
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many Solutions Does This Equation Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
