Common Multiples Of 4 And 5
Juapaving
Apr 02, 2025 · 6 min read
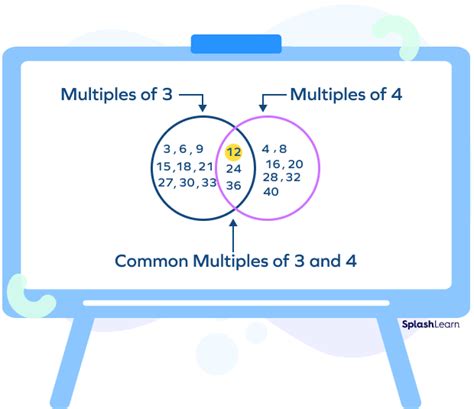
Table of Contents
- Common Multiples Of 4 And 5
- Table of Contents
- Unveiling the Secrets of Common Multiples of 4 and 5: A Deep Dive
- Understanding Multiples
- Identifying Common Multiples
- Finding Common Multiples: The Listing Method
- Finding Common Multiples: The Prime Factorization Method
- Least Common Multiple (LCM) and Greatest Common Divisor (GCD)
- Applications of Common Multiples
- Exploring Further: Common Multiples Beyond 4 and 5
- Conclusion: Mastering Common Multiples
- Latest Posts
- Latest Posts
- Related Post
Unveiling the Secrets of Common Multiples of 4 and 5: A Deep Dive
Finding common multiples might seem like a simple arithmetic task, but understanding the underlying principles opens doors to more complex mathematical concepts. This comprehensive guide delves into the world of common multiples, focusing specifically on the common multiples of 4 and 5. We'll explore various methods for identifying these multiples, delve into their properties, and even touch upon their applications in real-world scenarios. Prepare to unlock a deeper understanding of this fundamental mathematical concept!
Understanding Multiples
Before we dive into the specifics of common multiples of 4 and 5, let's establish a solid foundation. A multiple of a number is the result of multiplying that number by any whole number (integer). For instance:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, and so on.
Notice how the multiples of a number extend infinitely in both positive and negative directions. However, we typically focus on the positive multiples.
Identifying Common Multiples
A common multiple is a number that is a multiple of two or more numbers. In our case, we're interested in the common multiples of 4 and 5. Looking at the lists above, we can already identify some:
- 20 is a multiple of 4 (4 x 5 = 20) and a multiple of 5 (5 x 4 = 20).
- 40 is a multiple of 4 (4 x 10 = 40) and a multiple of 5 (5 x 8 = 40).
- 60 is a multiple of 4 (4 x 15 = 60) and a multiple of 5 (5 x 12 = 60).
These are just a few examples; there are infinitely many common multiples of 4 and 5.
Finding Common Multiples: The Listing Method
The method we used above, visually comparing lists of multiples, is effective for smaller numbers but becomes cumbersome for larger numbers. Let's explore more efficient techniques. The listing method, while simple, involves writing out a substantial number of multiples for each number until common multiples are identified. This approach works best for smaller numbers and helps visualize the concept.
Finding Common Multiples: The Prime Factorization Method
A more powerful technique involves prime factorization. This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Factor the numbers:
- 4 = 2 x 2 = 2²
- 5 = 5
-
Find the highest power of each prime factor:
- The prime factors are 2 and 5. The highest power of 2 is 2², and the highest power of 5 is 5¹.
-
Multiply the highest powers:
- 2² x 5 = 4 x 5 = 20
This reveals that the least common multiple (LCM) of 4 and 5 is 20. All other common multiples are multiples of the LCM. Therefore, the common multiples of 4 and 5 are 20, 40, 60, 80, 100, and so on. This is a significantly more efficient method than the listing method, especially when dealing with larger numbers.
Least Common Multiple (LCM) and Greatest Common Divisor (GCD)
The least common multiple (LCM) is the smallest positive integer that is a multiple of all the given numbers. In our case, the LCM of 4 and 5 is 20. Understanding the LCM is crucial for various mathematical operations, including fraction simplification and solving problems involving ratios and proportions.
Conversely, the greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest positive integer that divides all the given numbers without leaving a remainder. The GCD of 4 and 5 is 1, as they share no common factors other than 1. The relationship between LCM and GCD is expressed by the formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. This formula offers another method to calculate the LCM if the GCD is known.
Applications of Common Multiples
The concept of common multiples finds applications in various real-world scenarios:
-
Scheduling: Imagine two buses that depart from the same station. One bus departs every 4 hours, and the other departs every 5 hours. Finding the common multiples of 4 and 5 helps determine when both buses will depart at the same time. The next common departure time will be in 20 hours.
-
Pattern Recognition: Common multiples appear in repeating patterns. Consider arranging tiles in a rectangular grid. If you have tiles of size 4 units x 4 units, and another size of 5 units x 5 units, the smallest square grid you can form using only these tiles has sides measuring 20 units.
-
Fraction Operations: Determining the least common denominator (LCD) when adding or subtracting fractions requires finding the LCM of the denominators. For example, adding 1/4 and 1/5 requires finding the LCM of 4 and 5 (which is 20) and then converting the fractions to have a common denominator before adding them.
-
Gear Ratios: In mechanical engineering, gear ratios often involve common multiples to ensure smooth and efficient operation.
Exploring Further: Common Multiples Beyond 4 and 5
The principles discussed for finding common multiples of 4 and 5 extend to any set of numbers. The prime factorization method remains a powerful tool, even for larger numbers. Let's consider an example: finding the common multiples of 6, 8, and 12.
-
Prime Factorization:
- 6 = 2 x 3
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
-
Highest Powers:
- The prime factors are 2 and 3. The highest power of 2 is 2³, and the highest power of 3 is 3¹.
-
LCM Calculation:
- 2³ x 3 = 8 x 3 = 24
Therefore, the LCM of 6, 8, and 12 is 24. All common multiples of 6, 8, and 12 are multiples of 24.
Conclusion: Mastering Common Multiples
Understanding common multiples is a cornerstone of number theory and has far-reaching applications in various fields. This guide has explored different methods for identifying common multiples, focusing on the numbers 4 and 5, and generalized the concepts to encompass any set of integers. The prime factorization method, in particular, provides an efficient and powerful tool for calculating the least common multiple (LCM), which is fundamental to solving numerous mathematical problems and understanding real-world phenomena. By mastering these concepts, you will enhance your mathematical skills and gain a deeper appreciation of the interconnectedness of numbers and their properties. So, continue exploring the fascinating world of numbers and discover the hidden patterns and relationships that make mathematics such a captivating subject!
Latest Posts
Latest Posts
-
Compare And Contrast Facilitated Diffusion And Active Transport
Apr 05, 2025
-
Find The Lcm Of 6 And 14
Apr 05, 2025
-
Cellulose Cannot Be Digested By Humans
Apr 05, 2025
-
A Thin Uniform Rod Of Length L
Apr 05, 2025
-
5 Letter Word Ends With Eat
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
