How Many Sides A Rectangle Has
Juapaving
Mar 27, 2025 · 6 min read
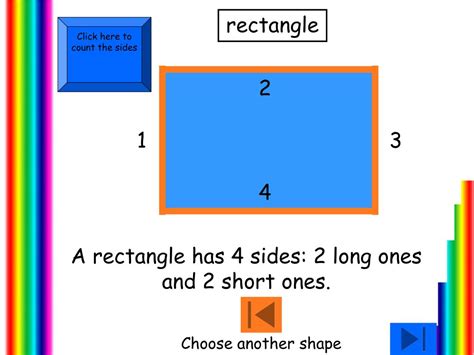
Table of Contents
How Many Sides Does a Rectangle Have? A Deep Dive into Geometry
The question, "How many sides does a rectangle have?" might seem trivial at first glance. The answer, of course, is four. But a simple question can open doors to a fascinating exploration of geometry, its properties, and its applications in the real world. This article delves beyond the simple answer, exploring the defining characteristics of rectangles, comparing them to other quadrilaterals, and examining their significance in various fields.
Understanding the Fundamentals: Defining a Rectangle
Before we dive deeper, let's establish a clear understanding of what constitutes a rectangle. A rectangle is a two-dimensional shape defined by four sides and four right angles (90-degree angles). These four sides are arranged to form a closed shape, with opposite sides being equal in length. This characteristic of having equal opposite sides is a crucial defining feature of a rectangle, differentiating it from other quadrilaterals.
Key Properties of a Rectangle:
-
Four Sides: This is the most fundamental characteristic. The presence of four sides is the starting point for classifying a shape as a quadrilateral, a broader category that includes rectangles, squares, parallelograms, and trapezoids.
-
Four Right Angles: Each of the four interior angles measures exactly 90 degrees. This is what distinguishes a rectangle from other quadrilaterals that might have four sides but lack the right angles.
-
Opposite Sides are Equal: The lengths of opposite sides are always equal. This means if you measure one side of the rectangle and then the side opposite it, they will have the same length. This property is crucial in calculating the perimeter and area of a rectangle.
-
Parallel Opposite Sides: The opposite sides of a rectangle are parallel to each other. This parallel nature contributes to the stability and predictable properties of the rectangle.
Rectangles vs. Other Quadrilaterals: Spotting the Differences
Understanding rectangles requires comparing them to other quadrilaterals. This comparison helps highlight the unique properties that set rectangles apart.
Rectangle vs. Square: Subtle Yet Significant Differences
A square is a special type of rectangle. All squares are rectangles, but not all rectangles are squares. The key difference lies in the length of the sides. In a square, all four sides are equal in length. A rectangle, on the other hand, only requires that opposite sides are equal. Therefore, a square satisfies all the conditions of a rectangle, but a rectangle doesn't necessarily satisfy all conditions of a square.
Rectangle vs. Parallelogram: The Angle Makes the Difference
Both rectangles and parallelograms have opposite sides that are equal and parallel. However, the defining difference lies in the angles. A parallelogram only requires opposite sides to be parallel and equal; its angles are not necessarily right angles. A rectangle is a special type of parallelogram where all four angles are right angles.
Rectangle vs. Trapezoid: Parallel Sides and Beyond
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. Unlike rectangles, trapezoids don't necessarily have equal opposite sides or right angles. A rectangle, therefore, is a much more restrictive and specific type of quadrilateral.
The Significance of Rectangles: Real-World Applications
Rectangles are far from being mere geometric abstractions; they are fundamental shapes with widespread applications in various aspects of life:
Architecture and Construction:
Rectangles form the basis of many structures. Buildings, rooms, windows, and doors are often rectangular in shape due to the stability and efficiency this shape provides. The rectangular structure is easily reproducible, cost-effective, and allows for simple calculations related to area and volume.
Engineering and Design:
Rectangular shapes are prevalent in engineering designs due to their structural strength and ease of fabrication. From bridges and roadways to electronic components and furniture, the rectangular form offers both practicality and aesthetics.
Art and Design:
In art and graphic design, rectangles are fundamental compositional elements. The use of rectangular frames and canvases provides a structured and balanced aesthetic, helping artists create visual harmony and focus.
Everyday Objects:
Countless everyday objects are rectangular: books, computer screens, televisions, tables, and countless others. The prevalence of this shape reflects its practicality and versatility.
Calculating Properties of Rectangles: Area and Perimeter
The simple answer to "How many sides does a rectangle have?" leads to more complex calculations. Two important properties frequently calculated for rectangles are area and perimeter.
Calculating the Perimeter of a Rectangle:
The perimeter of a rectangle is the total distance around its four sides. Because opposite sides are equal, the formula for the perimeter (P) is:
P = 2(length + width)
This formula allows for easy calculation of the perimeter given the length and width of the rectangle.
Calculating the Area of a Rectangle:
The area of a rectangle represents the space enclosed within its four sides. The formula for the area (A) is:
A = length × width
This simple formula is widely used in various applications, from calculating floor space to determining the amount of material needed for a project.
Beyond the Basics: Exploring Advanced Concepts
The seemingly simple question about the number of sides in a rectangle opens up avenues for exploring more advanced geometrical concepts.
Diagonal of a Rectangle:
The diagonal of a rectangle connects two opposite corners. The length of the diagonal can be calculated using the Pythagorean theorem:
d² = length² + width²
where 'd' represents the length of the diagonal. This calculation is frequently used in various applications such as determining distances or dimensions in construction or design.
Similar Rectangles:
Similar rectangles share the same ratio between their corresponding sides. This concept is used in scaling, map-making, and model building, allowing for accurate representation of larger structures or areas.
Tessellations: Covering Surfaces with Rectangles
Rectangles tessellate perfectly, meaning they can be arranged to cover a surface completely without gaps or overlaps. This property is utilized in tiling, flooring, and paving designs. The simple geometric pattern created by tessellating rectangles provides both visual appeal and efficiency in covering surfaces.
Conclusion: The Enduring Importance of Rectangles
The seemingly simple question of how many sides a rectangle has unveils a rich tapestry of geometric concepts, real-world applications, and mathematical principles. From its foundational role in geometry to its widespread use in architecture, engineering, and everyday life, the rectangle remains a cornerstone shape, demonstrating its enduring importance in our understanding of the world around us. Understanding its properties is not just an academic exercise; it's a key to unlocking practical solutions and appreciating the underlying structure of numerous objects and designs we encounter daily. The four sides of a rectangle thus represent far more than just a simple shape; they represent a foundation upon which much of our built and designed environment rests.
Latest Posts
Latest Posts
-
Is Souring Of Milk A Chemical Change
Mar 30, 2025
-
What Is The Least Common Multiple Of 7 14
Mar 30, 2025
-
What Is The Lcm Of 2 And 10
Mar 30, 2025
-
Why Is Water Considered To Be A Renewable Resource
Mar 30, 2025
-
Find The Area Under The Curve Calculator
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides A Rectangle Has . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
