How Many Diagonals Does A Triangle Have
Juapaving
Mar 25, 2025 · 5 min read
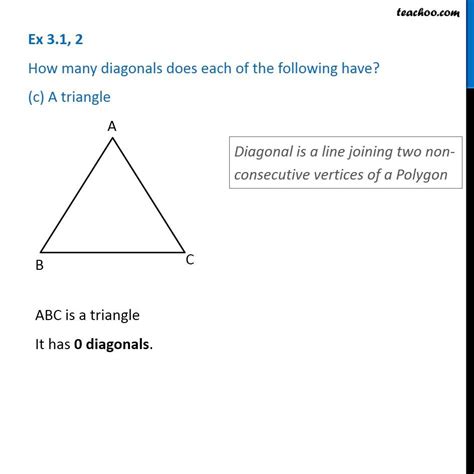
Table of Contents
How Many Diagonals Does a Triangle Have? A Comprehensive Exploration
The seemingly simple question, "How many diagonals does a triangle have?" often serves as a gateway to understanding fundamental geometric concepts. While the answer might seem immediately obvious to some, a deeper dive reveals opportunities to explore related mathematical ideas and appreciate the elegance of geometric principles. This comprehensive guide will not only answer the question but also explore the broader context of diagonals in polygons, solidifying your understanding of these essential geometric concepts.
Understanding Diagonals
Before we tackle the triangle specifically, let's establish a clear definition of a diagonal. In geometry, a diagonal is a line segment connecting two non-adjacent vertices of a polygon. Non-adjacent means the vertices are not directly next to each other along the polygon's perimeter. This seemingly simple definition is crucial for understanding the concept's application to various polygons.
Consider a simple quadrilateral (a four-sided polygon). It has two diagonals. Imagine connecting opposite corners; those lines are diagonals. Now, visualize a pentagon (five-sided polygon). It has five vertices, and from each vertex, you can draw diagonals to two other non-adjacent vertices, resulting in a total of five diagonals. The pattern, however, isn't as simple as it initially appears. As the number of sides increases, the number of diagonals grows at a faster rate.
The Case of the Triangle: A Unique Polygon
A triangle, being a polygon with three sides and three vertices, presents a unique case. Let's revisit the definition of a diagonal: a line segment joining two non-adjacent vertices. In a triangle, all vertices are adjacent to each other. There's no pair of vertices that are not directly connected by a side. Therefore, a triangle has zero diagonals.
This seemingly straightforward answer underscores a crucial aspect of geometric reasoning: the application of definitions. Understanding the precise definition of a diagonal is key to determining its presence or absence in different polygons. The absence of diagonals in a triangle is not an exception; it's a direct consequence of the definition itself.
Exploring the Formula for Diagonals in Polygons
The number of diagonals in a polygon with 'n' sides can be calculated using a specific formula. This formula helps us understand the relationship between the number of sides and the number of diagonals and further reinforces the uniqueness of the triangle's case.
The formula for the number of diagonals (D) in a polygon with 'n' sides is:
D = n(n - 3) / 2
Let's apply this formula to various polygons:
-
Triangle (n = 3): D = 3(3 - 3) / 2 = 0. This confirms our earlier conclusion.
-
Quadrilateral (n = 4): D = 4(4 - 3) / 2 = 2. This confirms the two diagonals in a quadrilateral.
-
Pentagon (n = 5): D = 5(5 - 3) / 2 = 5. This matches our visualization of the pentagon's diagonals.
-
Hexagon (n = 6): D = 6(6 - 3) / 2 = 9.
This formula provides a systematic way to determine the number of diagonals for any polygon, highlighting the special case of the triangle, where the formula yields zero.
Why the Formula Works: A Combinatorial Approach
The formula for the number of diagonals can be derived using combinatorial principles. We start by considering the number of ways to choose two vertices from a polygon with 'n' vertices. This is given by the combination formula:
n C 2 = n! / (2!(n - 2)!) = n(n - 1) / 2
This formula calculates the total number of line segments that can be drawn between any two vertices, including the sides of the polygon. To get the number of diagonals, we must subtract the number of sides ('n') from this total:
D = n(n - 1) / 2 - n = n(n - 1) / 2 - 2n/2 = n(n - 3) / 2
This derivation demonstrates the mathematical elegance behind the formula and provides a more rigorous understanding of its application. Again, the triangle's case highlights the critical role of subtracting the sides to isolate only the diagonals.
Diagonals and Geometric Properties
The presence or absence of diagonals impacts several geometric properties. For example, diagonals can be used to divide polygons into smaller triangles, a technique used in calculating the area of irregular polygons. In quadrilaterals, the properties of diagonals (e.g., their lengths, points of intersection) determine the type of quadrilateral (e.g., parallelogram, rectangle, rhombus, square).
The lack of diagonals in a triangle, however, doesn't diminish its significance. Triangles are the fundamental building blocks of many geometric constructions, possessing unique properties like the triangle inequality theorem and the ability to be uniquely determined by three sides (SSS), two sides and an included angle (SAS), two angles and an included side (ASA), or a combination of these. These properties make triangles incredibly useful in diverse fields of mathematics and applications like surveying, architecture, and engineering.
Beyond the Triangle: Exploring Other Polygons
Let's briefly explore the diagonal properties of other polygons:
-
Quadrilaterals: The diagonals of a quadrilateral can intersect, creating four smaller triangles. The properties of these diagonals define the quadrilateral's type.
-
Pentagons: Pentagons have five diagonals, forming a complex star-like pattern within the polygon.
-
Regular Polygons: In regular polygons (polygons with all sides and angles equal), the diagonals exhibit interesting symmetry and patterns, providing avenues for further geometric exploration.
Practical Applications of Diagonals
The concept of diagonals isn't just a theoretical exercise. It finds application in various fields:
-
Computer Graphics: Diagonals are used in algorithms for rendering polygons and creating 3D models.
-
Engineering: Understanding diagonal bracing in structures is crucial for ensuring stability and strength.
-
Cartography: Diagonals can be used to create efficient triangulation for surveying and map-making.
-
Architecture: The diagonal support in buildings enhances structural integrity.
Conclusion: The Significance of the Zero Diagonals in a Triangle
The seemingly simple question of how many diagonals a triangle has leads to a deeper understanding of fundamental geometric concepts, including the precise definition of a diagonal, the derivation of formulas, and the broader implications of these concepts in diverse fields. The fact that a triangle has zero diagonals isn't a deficiency; it's a unique characteristic that emphasizes the fundamental building block nature of triangles in geometry and its countless applications. The exploration of this seemingly simple question illuminates the power of precise mathematical definitions and the interconnectedness of geometric ideas. The absence of diagonals in a triangle highlights the polygon's inherent stability and its significant role in various geometric and practical applications. It's a testament to the beauty and elegance of mathematical principles.
Latest Posts
Latest Posts
-
Which Of The Following Are True About Algae
Mar 28, 2025
-
Which Region Of The Nephron Is Impermeable To Water
Mar 28, 2025
-
What Is The Lcm Of 7 21
Mar 28, 2025
-
In The Periodic Table Horizontal Rows Are Called
Mar 28, 2025
-
Why Does The Pupil Of The Eye Appear Black
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How Many Diagonals Does A Triangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
