Highest Common Factor Of 40 And 25
Juapaving
Mar 21, 2025 · 5 min read
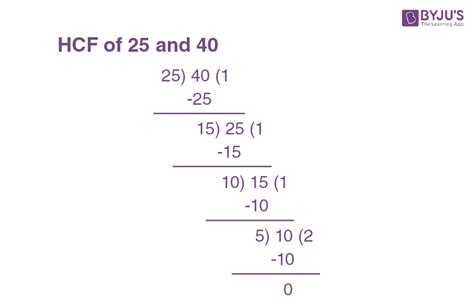
Table of Contents
Finding the Highest Common Factor (HCF) of 40 and 25: A Deep Dive
The highest common factor (HCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. Finding the HCF is a fundamental concept in mathematics with applications in various fields, from simplifying fractions to solving complex algebraic problems. This article will delve deep into finding the HCF of 40 and 25, exploring multiple methods and illustrating the underlying principles. We will also explore the broader context of HCF and its significance in mathematics.
Understanding the Concept of Highest Common Factor (HCF)
Before we embark on calculating the HCF of 40 and 25, let's solidify our understanding of the concept. The HCF is essentially the largest number that is a common factor of two or more numbers. A factor is a number that divides another number completely without leaving any remainder.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. Therefore, the highest common factor (HCF) of 12 and 18 is 6.
Method 1: Prime Factorization Method
This method involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). Once we have the prime factorization of both numbers, we identify the common prime factors and multiply them together to find the HCF.
Let's apply this to 40 and 25:
1. Prime Factorization of 40:
40 = 2 x 2 x 2 x 5 = 2³ x 5
2. Prime Factorization of 25:
25 = 5 x 5 = 5²
3. Identifying Common Prime Factors:
Both 40 and 25 share one common prime factor: 5.
4. Calculating the HCF:
The HCF is the product of the common prime factors. In this case, the HCF of 40 and 25 is 5.
Method 2: Division Method (Euclidean Algorithm)
The Euclidean algorithm is an efficient method for finding the HCF, particularly useful for larger numbers. This method involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the HCF.
Let's apply the Euclidean algorithm to 40 and 25:
1. Divide the larger number (40) by the smaller number (25):
40 ÷ 25 = 1 with a remainder of 15
2. Replace the larger number with the remainder (15) and repeat the division:
25 ÷ 15 = 1 with a remainder of 10
3. Repeat the process:
15 ÷ 10 = 1 with a remainder of 5
4. Repeat again:
10 ÷ 5 = 2 with a remainder of 0
5. The HCF is the last non-zero remainder:
The last non-zero remainder is 5. Therefore, the HCF of 40 and 25 is 5.
Method 3: Listing Factors Method
This method involves listing all the factors of each number and then identifying the common factors. The largest common factor is the HCF. While this method is straightforward for smaller numbers, it becomes cumbersome for larger numbers.
1. Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
2. Factors of 25: 1, 5, 25
3. Common Factors: 1, 5
4. HCF: The highest common factor is 5.
Applications of HCF
The concept of the highest common factor has numerous applications across various mathematical fields and real-world scenarios. Here are some key applications:
-
Simplifying Fractions: The HCF is crucial in simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their HCF. For example, the fraction 40/25 can be simplified to 8/5 by dividing both the numerator and denominator by their HCF, which is 5.
-
Solving Word Problems: Many word problems involving division and sharing require finding the HCF to determine the largest possible equal groups or quantities.
-
Algebra and Number Theory: HCF plays a significant role in advanced mathematical concepts like modular arithmetic, Diophantine equations, and abstract algebra.
-
Geometry: HCF finds applications in geometry, for example, in finding the dimensions of the largest possible square tile that can perfectly cover a rectangular floor without any gaps or overlaps.
Understanding the Relationship between LCM and HCF
The least common multiple (LCM) is another important concept closely related to the HCF. The LCM is the smallest number that is a multiple of two or more numbers. There's a crucial relationship between the HCF and LCM of two numbers (a and b):
LCM(a, b) x HCF(a, b) = a x b
This formula allows us to calculate the LCM if we know the HCF, and vice-versa. For 40 and 25, we found the HCF to be 5. Let's use the formula to find the LCM:
LCM(40, 25) x 5 = 40 x 25 LCM(40, 25) = (40 x 25) / 5 LCM(40, 25) = 200
Choosing the Right Method
The best method for finding the HCF depends on the numbers involved. For smaller numbers, the listing factors method might be sufficient. However, for larger numbers, the prime factorization method or the Euclidean algorithm is more efficient and less prone to errors. The Euclidean algorithm is particularly advantageous for very large numbers as it avoids the potentially tedious task of finding all prime factors.
Conclusion: The Significance of HCF
The highest common factor (HCF) is a fundamental concept in number theory with far-reaching applications in mathematics and beyond. Understanding different methods for calculating the HCF equips us with valuable tools to solve various mathematical problems and appreciate the interconnectedness of seemingly disparate mathematical ideas. Whether you use the prime factorization method, the Euclidean algorithm, or the listing factors method, the ability to find the HCF efficiently is a cornerstone of mathematical proficiency. The example of finding the HCF of 40 and 25 provides a solid foundation for understanding this vital concept and its implications. Remember, mastering the concept of HCF opens doors to a deeper understanding of more complex mathematical structures and applications.
Latest Posts
Latest Posts
-
Words With Ie In Them 5 Letters
Mar 27, 2025
-
What Are The Pros Of Fossil Fuels
Mar 27, 2025
-
An Object Following A Straight Line Path At Constant Speed
Mar 27, 2025
-
Is Ice Cream Melting A Physical Change
Mar 27, 2025
-
Why Does Electronegativity Increase From Left To Right
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 40 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
