Greatest Common Factor For 36 And 90
Juapaving
Apr 01, 2025 · 5 min read
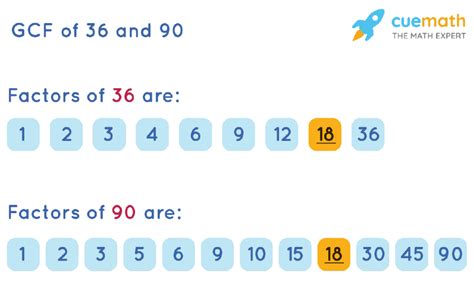
Table of Contents
- Greatest Common Factor For 36 And 90
- Table of Contents
- Finding the Greatest Common Factor (GCF) of 36 and 90: A Comprehensive Guide
- Understanding the Greatest Common Factor (GCF)
- Method 1: Listing Factors
- Method 2: Prime Factorization
- Method 3: Euclidean Algorithm
- Applications of Finding the GCF
- Extending the Concept: GCF of More Than Two Numbers
- Conclusion: Mastering the GCF
- Latest Posts
- Latest Posts
- Related Post
Finding the Greatest Common Factor (GCF) of 36 and 90: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more numbers is a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will delve into the various methods of determining the GCF, focusing specifically on the numbers 36 and 90. We'll explore multiple approaches, from the basic listing of factors to more advanced techniques, solidifying your understanding of this crucial mathematical principle.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of the numbers without leaving a remainder. It's essentially the largest number that is a factor of all the given numbers. Understanding the concept of factors is crucial before we begin calculating the GCF. A factor is a number that divides another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers like 36 and 90. Let's list the factors of each number:
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Now, compare the two lists. Identify the common factors – the numbers that appear in both lists.
Common Factors of 36 and 90: 1, 2, 3, 6, 9, 18
The largest number in this list of common factors is 18. Therefore, the GCF of 36 and 90 is 18.
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method, especially for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
Prime Factorization of 90:
90 = 2 x 45 = 2 x 3 x 15 = 2 x 3 x 3 x 5 = 2 x 3² x 5
Now, identify the common prime factors and their lowest powers:
Both 36 and 90 share a factor of 2 (to the power of 1) and 3 (to the power of 2).
Therefore, the GCF is 2¹ x 3² = 2 x 9 = 18
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 36 and 90:
- 90 ÷ 36 = 2 with a remainder of 18
- Now, we replace the larger number (90) with the remainder (18): The new pair is 36 and 18.
- 36 ÷ 18 = 2 with a remainder of 0
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 18.
Applications of Finding the GCF
The GCF has numerous practical applications across various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 36/90 can be simplified by dividing both the numerator and the denominator by their GCF (18), resulting in the simplified fraction 2/5.
-
Solving Word Problems: Many word problems in algebra and number theory involve finding the GCF. For instance, problems related to distributing items equally among groups often require finding the GCF to determine the maximum number of items each group can receive.
-
Geometry: The GCF can be used to determine the dimensions of the largest square tile that can be used to completely cover a rectangular area without any gaps or overlaps.
-
Computer Science: The GCF is used in various algorithms and computations in computer science, particularly in cryptography and number theory.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with their lowest powers. For the Euclidean algorithm, you would apply it iteratively to pairs of numbers.
For instance, let's find the GCF of 36, 90, and 108:
- Prime Factorization of 36: 2² x 3²
- Prime Factorization of 90: 2 x 3² x 5
- Prime Factorization of 108: 2² x 3³
The common prime factors are 2 and 3. The lowest powers are 2¹ and 3². Therefore, the GCF of 36, 90, and 108 is 2 x 9 = 18.
Conclusion: Mastering the GCF
Understanding and efficiently calculating the greatest common factor is a valuable skill in mathematics. This guide has explored various methods, from the simple listing of factors to the more advanced Euclidean algorithm, providing you with a comprehensive toolkit for tackling GCF problems. Whether you're simplifying fractions, solving word problems, or delving into more advanced mathematical concepts, mastering the GCF will significantly enhance your mathematical abilities. Remember to choose the method best suited to the numbers you are working with, prioritizing efficiency and understanding. The examples provided, focusing specifically on the numbers 36 and 90, have illuminated the process step-by-step, enabling you to confidently apply these techniques in various mathematical contexts. Continue practicing, and you'll find calculating the GCF becomes second nature.
Latest Posts
Latest Posts
-
What Is The Only Movable Bone In The Skull
Apr 06, 2025
-
How Big Is 40 Cm In Inches
Apr 06, 2025
-
Decimal Greater Than And Less Than
Apr 06, 2025
-
A Solids Volume And Shape Is Defintie
Apr 06, 2025
-
Can A Scalene Triangle Be Obtuse
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor For 36 And 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
