Greatest Common Factor 36 And 90
Juapaving
Mar 31, 2025 · 6 min read
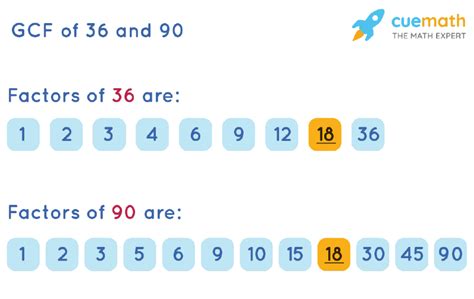
Table of Contents
Greatest Common Factor of 36 and 90: A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with wide-ranging applications in mathematics and beyond. This article will explore the GCF of 36 and 90 in detail, explaining multiple methods for finding it, and then delving into the significance of this seemingly simple calculation. We'll uncover its importance in simplifying fractions, solving algebraic problems, and even understanding more advanced mathematical concepts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For instance, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest of these is 6, making 6 the GCF of 12 and 18.
This seemingly straightforward concept forms the basis for many important mathematical operations and problem-solving techniques. Understanding the GCF is crucial for simplifying fractions to their lowest terms, factoring polynomials, and solving various problems in algebra and number theory.
Finding the GCF of 36 and 90: Three Proven Methods
Let's now focus on finding the GCF of 36 and 90. We'll explore three common methods:
1. Listing Factors Method
This method is straightforward and easy to understand, especially for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
By comparing the two lists, we can see that the common factors are 1, 2, 3, 6, 9, and 18. The greatest among these is 18. Therefore, the GCF of 36 and 90 is 18.
This method works well for smaller numbers, but it can become cumbersome and time-consuming for larger numbers with many factors.
2. Prime Factorization Method
This method is more efficient, particularly for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime factorization of 36: 2² x 3² (36 = 2 x 2 x 3 x 3)
Prime factorization of 90: 2 x 3² x 5 (90 = 2 x 3 x 3 x 5)
Now, we identify the common prime factors: 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3². Therefore, the GCF is 2¹ x 3² = 2 x 9 = 18.
This method is more systematic and less prone to errors, especially when dealing with larger numbers. It's a highly recommended approach for its efficiency and accuracy.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 36 and 90:
- 90 - 36 = 54 (Now we find the GCF of 36 and 54)
- 54 - 36 = 18 (Now we find the GCF of 36 and 18)
- 36 - 18 = 18 (The numbers are now equal)
Therefore, the GCF of 36 and 90 is 18.
The Euclidean algorithm is particularly efficient for large numbers because it significantly reduces the number of calculations compared to the other methods. It's a powerful tool in number theory and has many applications beyond just finding the GCF.
Applications of the GCF: Beyond Simple Arithmetic
The GCF, seemingly a basic mathematical concept, has far-reaching implications in various areas of mathematics and even beyond:
1. Simplifying Fractions
The GCF is essential for simplifying fractions to their lowest terms. Consider the fraction 36/90. Since the GCF of 36 and 90 is 18, we can simplify the fraction by dividing both the numerator and the denominator by 18:
36/90 = (36 ÷ 18) / (90 ÷ 18) = 2/5
This process ensures that the fraction is represented in its simplest form, making it easier to work with and understand.
2. Solving Algebraic Equations
The GCF plays a crucial role in factoring polynomials. Factoring allows us to simplify algebraic expressions and solve equations more easily. For instance, consider the expression 36x + 90y. The GCF of 36 and 90 is 18, so we can factor out 18:
36x + 90y = 18(2x + 5y)
This factored form is often more useful in solving equations and performing other algebraic manipulations.
3. Least Common Multiple (LCM) Calculation
The GCF is closely related to the least common multiple (LCM). The LCM is the smallest positive integer that is divisible by both numbers. There's a useful relationship between the GCF and LCM:
LCM(a, b) x GCF(a, b) = a x b
Knowing the GCF allows us to quickly calculate the LCM. In the case of 36 and 90, the GCF is 18. Therefore:
LCM(36, 90) = (36 x 90) / 18 = 180
The LCM is crucial for various applications, including adding and subtracting fractions with different denominators and solving problems involving periodic events.
4. Applications in Computer Science and Cryptography
The Euclidean algorithm, used for finding the GCF, is a fundamental algorithm in computer science. It's used in various applications, including cryptography, where it plays a critical role in RSA encryption, a widely used public-key cryptosystem.
5. Modular Arithmetic and Number Theory
GCF is foundational in modular arithmetic, a branch of number theory. Concepts like modular inverses, essential for cryptography and other number-theoretic computations, rely heavily on the GCF.
Conclusion: The Unsung Hero of Number Theory
The greatest common factor, while seemingly a simple concept, is a fundamental building block in numerous areas of mathematics. From simplifying fractions to solving complex algebraic equations and even playing a crucial role in modern cryptography, the GCF’s significance extends far beyond basic arithmetic. Mastering the various methods for calculating the GCF, such as the listing factors method, prime factorization method, and the highly efficient Euclidean algorithm, provides a solid foundation for tackling more advanced mathematical problems and applications. Its importance underscores the power of seemingly simple concepts in unlocking deeper mathematical understanding and solving real-world problems. The GCF is indeed an unsung hero of number theory, quietly underpinning a wide range of mathematical operations and applications.
Latest Posts
Latest Posts
-
What Is Group Of Baboons Called
Apr 02, 2025
-
Exterior Angle Of A Regular Octagon
Apr 02, 2025
-
What Are The Common Multiples Of 24
Apr 02, 2025
-
Give The Iupac Name For The Following Compound
Apr 02, 2025
-
The Units Of Measurement For Voltage Is The
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor 36 And 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
