Given A 120 Degree Angle Construct A 0 Degree Angl
Juapaving
Mar 31, 2025 · 5 min read
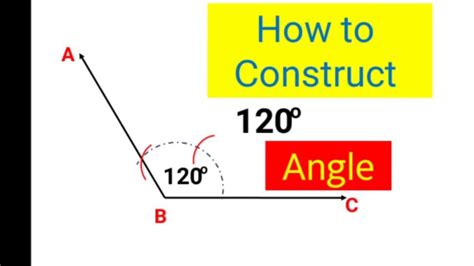
Table of Contents
Constructing a 0-Degree Angle from a 120-Degree Angle: A Comprehensive Guide
Constructing a 0-degree angle, essentially a straight line, from a given 120-degree angle might seem trivial at first glance. After all, a straight line is the simplest geometric form. However, the process involves understanding fundamental geometric principles and employing accurate construction techniques. This comprehensive guide will explore various methods, emphasizing precision and clarity for both beginners and experienced geometers. We will delve into the underlying mathematical concepts and practical applications, ensuring a thorough understanding of this seemingly simple task.
Understanding the Fundamentals: Angles and Their Construction
Before we embark on the construction process, let's refresh our understanding of angles and their properties. An angle is formed by two rays (or line segments) that share a common endpoint, called the vertex. Angles are measured in degrees, with a complete revolution around a point equaling 360 degrees. A 0-degree angle, representing collinearity, implies that the two rays lie on the same line, extending in opposite directions.
A 120-degree angle, on the other hand, represents one-third of a full rotation. Our task is to utilize this given 120-degree angle to construct its inverse – a perfectly straight 0-degree angle.
Method 1: Bisecting the 120-Degree Angle Twice
This is the most straightforward and commonly used method. It relies on the principle of angle bisection – dividing an angle into two equal halves.
Step 1: Bisecting the 120-Degree Angle
Using a compass, draw an arc with the vertex of the 120-degree angle as the center. This arc should intersect both rays forming the angle. Let's call these intersection points A and B.
Now, keeping the compass at the same radius, place the compass point on A and draw another arc. Repeat this process with the compass point on B, ensuring the arcs intersect. The point where these two arcs intersect will lie on the angle bisector. Draw a ray from the vertex through this intersection point. This ray perfectly bisects the 120-degree angle, creating two 60-degree angles.
Step 2: Bisecting a 60-Degree Angle
We now have two 60-degree angles. We select one of them and repeat the bisection process. Draw an arc from the vertex intersecting both rays of the 60-degree angle. Using the same radius, place the compass point on each intersection point and draw arcs that intersect. A ray drawn from the vertex through the intersection of these arcs bisects the 60-degree angle, creating two 30-degree angles.
Step 3: Achieving the 0-Degree Angle
By bisecting the 120-degree angle twice, we have effectively created a 30-degree angle. The two rays forming this 30-degree angle, when extended, will create a straight line, essentially a 0-degree angle. This straight line perfectly represents the desired 0-degree angle constructed from the initial 120-degree angle. This method highlights the power of repetitive bisection in geometric constructions.
Method 2: Using Supplementary Angles
This method leverages the concept of supplementary angles. Supplementary angles are two angles whose sum equals 180 degrees.
Step 1: Finding the Supplementary Angle
Since we have a 120-degree angle, its supplementary angle is 180 - 120 = 60 degrees. This means that if we extend one of the rays of the 120-degree angle, we create a 60-degree angle adjacent to the original angle.
Step 2: Constructing the 60-Degree Angle
This step requires a compass and straightedge. From the vertex of the 120-degree angle, draw a ray extending one of the original rays. This will form a supplementary angle to the 120-degree angle.
Step 3: Forming the 0-Degree Angle
The extended ray, along with the other ray forming the original 120-degree angle, now forms a 180-degree angle – a straight line. This straight line represents the 0-degree angle. This method emphasizes the relationship between angles and their supplementary counterparts in geometric constructions. It is a more direct approach than the bisection method but might require a more precise understanding of supplementary angle properties.
Method 3: Using a Protractor (Less Precise)
While not a strictly geometric construction method, using a protractor offers a practical, albeit less precise, approach.
Step 1: Measuring the 120-Degree Angle
Place the protractor's center on the vertex of the 120-degree angle and align the base line with one of the rays.
Step 2: Finding the 0-Degree Line
Find the 180-degree mark on the protractor. Draw a line connecting the vertex to the 180-degree mark. This line will be exactly 180 degrees from the initial ray.
Step 3: Confirmation
This resulting line represents a 0-degree angle (a straight line). This method lacks the mathematical rigor of the previous methods but provides a quick, approximate solution if absolute precision is not critical. It should be used only for situations where minor imperfections are acceptable.
Practical Applications and Implications
The ability to construct a 0-degree angle from a given angle has numerous applications in various fields:
-
Engineering and Design: Precise angle construction is crucial in architecture, mechanical engineering, and civil engineering, ensuring the structural integrity and functionality of designed objects.
-
Computer-Aided Design (CAD): CAD software relies heavily on precise geometric constructions. The ability to generate straight lines from other angles forms the basis of many design operations.
-
Cartography and Surveying: Accurate angle measurements and constructions are fundamental in mapping and land surveying.
-
Robotics and Automation: Precise angle manipulation is essential in robotics for accurate movements and object manipulation.
-
Mathematics Education: Constructing angles provides a hands-on, practical approach to understanding geometric principles and developing spatial reasoning skills.
Conclusion: Mastering Geometric Constructions
Constructing a 0-degree angle from a 120-degree angle, although seemingly simple, highlights the importance of fundamental geometric principles and the precise application of construction techniques. The methods described above, ranging from repeated angle bisection to utilizing supplementary angles, provide various pathways to achieving this objective. The choice of method often depends on the context, the desired level of precision, and the available tools. Mastering these techniques not only improves geometric understanding but also enhances problem-solving skills applicable to various disciplines. The ability to visualize and manipulate angles accurately is a fundamental skill with broad practical implications. Therefore, practice and a strong foundation in geometric concepts are vital for achieving proficiency in this and similar geometric constructions.
Latest Posts
Latest Posts
-
Round 972381 89348 To The Nearest Thousand
Apr 02, 2025
-
Letters With A Line Of Symmetry
Apr 02, 2025
-
What Is The Domain Of A Polynomial
Apr 02, 2025
-
What Is The Least Common Multiple Of 11 And 3
Apr 02, 2025
-
What Is The Unit For Time In Physics
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Given A 120 Degree Angle Construct A 0 Degree Angl . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
