Give The Value Of Each Trigonometric Ratio
Juapaving
Apr 01, 2025 · 6 min read
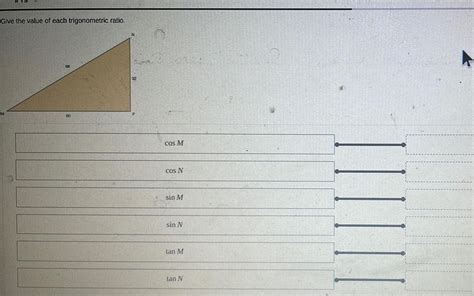
Table of Contents
Giving Value to Each Trigonometric Ratio: A Comprehensive Guide
Trigonometry, a cornerstone of mathematics, deals with the relationships between angles and sides of triangles. Understanding trigonometric ratios – sine, cosine, and tangent – is fundamental to solving a wide array of problems in various fields, from engineering and physics to computer graphics and surveying. This comprehensive guide will delve into the values of these ratios for key angles, explore their derivation, and highlight their applications.
Understanding the Trigonometric Ratios
Before diving into specific values, let's establish a clear understanding of what each ratio represents. Consider a right-angled triangle with a hypotenuse (the side opposite the right angle), an opposite side (the side opposite a given angle), and an adjacent side (the side next to the given angle).
-
Sine (sin): The sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse. sin θ = opposite/hypotenuse
-
Cosine (cos): The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. cos θ = adjacent/hypotenuse
-
Tangent (tan): The tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side. tan θ = opposite/adjacent
These ratios are interconnected. For example, the tangent of an angle can be expressed as the sine divided by the cosine: tan θ = sin θ / cos θ.
Trigonometric Ratios for Key Angles: 0°, 30°, 45°, 60°, and 90°
These five angles are particularly important because their trigonometric ratios have exact, easily remembered values, often expressed as fractions involving square roots. Let's examine each:
0°
- sin 0° = 0 (The opposite side of a 0° angle in a right-angled triangle has zero length.)
- cos 0° = 1 (The adjacent side becomes equal to the hypotenuse.)
- tan 0° = 0 (The opposite side has zero length, making the ratio zero.)
30°
To derive the values for 30°, consider an equilateral triangle with sides of length 2. Bisecting one angle creates a 30-60-90 triangle.
- sin 30° = 1/2 (Opposite side = 1, hypotenuse = 2)
- cos 30° = √3/2 (Adjacent side = √3, hypotenuse = 2)
- tan 30° = 1/√3 = √3/3 (Opposite side = 1, adjacent side = √3)
45°
A 45-45-90 triangle (an isosceles right-angled triangle) provides the values for 45°. If the legs have length 1, the hypotenuse is √2.
- sin 45° = 1/√2 = √2/2 (Opposite side = 1, hypotenuse = √2)
- cos 45° = 1/√2 = √2/2 (Adjacent side = 1, hypotenuse = √2)
- tan 45° = 1 (Opposite side = 1, adjacent side = 1)
60°
Returning to the 30-60-90 triangle from the 30° derivation:
- sin 60° = √3/2 (Opposite side = √3, hypotenuse = 2)
- cos 60° = 1/2 (Adjacent side = 1, hypotenuse = 2)
- tan 60° = √3 (Opposite side = √3, adjacent side = 1)
90°
- sin 90° = 1 (The opposite side becomes equal to the hypotenuse)
- cos 90° = 0 (The adjacent side has zero length)
- tan 90° = undefined (Division by zero is undefined)
Beyond the Key Angles: Using a Calculator or Trigonometric Tables
For angles other than these key values, you'll need a scientific calculator or trigonometric tables. These tools provide approximations of the trigonometric ratios for any angle. Remember to ensure your calculator is set to the correct angle mode (degrees or radians).
Applications of Trigonometric Ratios
The practical applications of trigonometric ratios are extensive and cross numerous disciplines:
1. Surveying and Mapping:
Trigonometric ratios are crucial for determining distances and heights indirectly. Surveyors use angles and known distances to calculate inaccessible distances, such as the width of a river or the height of a building.
2. Navigation:
In navigation, trigonometric ratios are used to calculate distances, bearings, and positions. For example, determining the distance to a landmark using its bearing and known distance.
3. Engineering and Construction:
Engineers rely heavily on trigonometry to design structures, analyze forces, and calculate angles in construction projects. This includes determining the strength and stability of bridges, buildings, and other infrastructure.
4. Physics:
Trigonometry plays a critical role in many areas of physics, including mechanics (resolving forces), optics (refraction and reflection), and electromagnetism (wave analysis).
5. Computer Graphics:
In computer graphics and animation, trigonometric functions are used extensively for creating realistic transformations, rotations, and projections. The accurate rendering of 3D objects relies heavily on these calculations.
6. Astronomy:
Astronomers use trigonometry to calculate distances to celestial bodies, determine their positions, and analyze their orbits. Parallax measurements, for instance, employ trigonometric principles.
Understanding the Unit Circle
The unit circle, a circle with a radius of 1 centered at the origin of a coordinate plane, provides a powerful visual representation of trigonometric ratios. For any angle θ, the x-coordinate represents cos θ, and the y-coordinate represents sin θ. This visualization helps in understanding the behavior of trigonometric functions and their periodic nature. The tangent is the ratio of the y-coordinate to the x-coordinate.
Inverse Trigonometric Functions
Inverse trigonometric functions (arcsin, arccos, arctan) find the angle whose trigonometric ratio is a given value. For example, arcsin(0.5) would return 30° (or π/6 radians). These inverse functions are essential for solving trigonometric equations and determining angles in various applications.
Reciprocal Trigonometric Functions
Besides sine, cosine, and tangent, there are three reciprocal trigonometric functions:
- Cosecant (csc): csc θ = 1/sin θ
- Secant (sec): sec θ = 1/cos θ
- Cotangent (cot): cot θ = 1/tan θ
These functions are useful in simplifying expressions and solving certain types of trigonometric equations.
Advanced Trigonometric Concepts
This guide has covered the basics, but trigonometry extends far beyond these fundamentals. More advanced concepts include:
- Trigonometric identities: Equations that are true for all angles. These identities are invaluable for simplifying expressions and solving equations.
- Trigonometric equations: Equations that involve trigonometric functions. Solving these equations requires a combination of algebraic techniques and trigonometric identities.
- Trigonometric graphs: Visual representations of trigonometric functions, illustrating their periodic nature and key features.
- Law of Sines and Law of Cosines: These laws extend trigonometric principles to non-right-angled triangles, allowing for the calculation of angles and sides in these more general scenarios.
Conclusion: Mastering the Fundamentals of Trigonometric Ratios
A solid grasp of trigonometric ratios is indispensable for success in many scientific and technical fields. This guide has provided a detailed explanation of the fundamental ratios, their values for key angles, and a glimpse into their extensive applications. By understanding these concepts and utilizing the appropriate tools (calculators, tables, or software), you'll be well-equipped to tackle a wide range of problems involving angles and triangles. Further exploration into advanced trigonometric concepts will only expand your ability to solve complex problems and apply this crucial mathematical toolset to real-world scenarios. Remember to practice regularly, and you’ll master the fascinating world of trigonometry in no time!
Latest Posts
Latest Posts
-
Least Common Multiple Of 20 And 30
Apr 02, 2025
-
Difference Between Starch Cellulose And Glycogen
Apr 02, 2025
-
What Is The Primary Function Of The Excretory System
Apr 02, 2025
-
How To Write 1300 On A Check
Apr 02, 2025
-
Examples Of Farewell Speech For Retirement
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Give The Value Of Each Trigonometric Ratio . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
