Formula For Perimeter Of Regular Polygon
Juapaving
Mar 27, 2025 · 5 min read
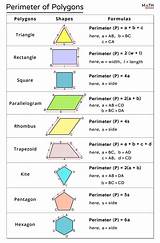
Table of Contents
The Definitive Guide to the Perimeter of a Regular Polygon
Understanding the perimeter of a regular polygon is fundamental in geometry and has wide-ranging applications in various fields. This comprehensive guide will delve deep into the formula, its derivation, practical applications, and related concepts. We'll explore different approaches to calculating the perimeter, cater to various skill levels, and offer numerous examples to solidify your understanding. By the end, you'll be confident in tackling any perimeter problem involving regular polygons.
What is a Regular Polygon?
Before diving into the perimeter formula, let's establish a clear understanding of what constitutes a regular polygon. A regular polygon is a closed two-dimensional figure with:
- Equal sides: All its sides have the same length.
- Equal angles: All its interior angles have the same measure.
Examples of regular polygons include:
- Equilateral Triangle (3 sides): The simplest regular polygon.
- Square (4 sides): A very common and familiar regular polygon.
- Regular Pentagon (5 sides): Used in various designs and architecture.
- Regular Hexagon (6 sides): Found in honeycombs and some crystals.
- Regular Heptagon (7 sides): Less common but still relevant in geometric studies.
- Regular Octagon (8 sides): Often seen in stop signs.
- And many more... The number of sides can extend infinitely.
The Formula for the Perimeter of a Regular Polygon
The formula for calculating the perimeter of a regular polygon is remarkably straightforward:
Perimeter = n * s
Where:
- n represents the number of sides in the polygon.
- s represents the length of one side of the polygon.
This formula leverages the fact that all sides of a regular polygon are equal in length. Therefore, multiplying the length of a single side by the total number of sides gives us the total perimeter.
Deriving the Formula: A Step-by-Step Approach
The formula's simplicity hides a fundamental geometric principle. Let's break down how it's derived:
-
Identify the sides: Begin by noting that a regular polygon possesses 'n' sides, all of equal length.
-
Represent the side length: Let 's' represent the length of each side.
-
Calculate the total perimeter: Since all sides are equal, the total perimeter is simply the sum of all side lengths: s + s + s + ... + s (repeated 'n' times).
-
Simplification using multiplication: This repeated addition can be efficiently expressed using multiplication: n * s.
This derivation highlights the elegance and efficiency of mathematical notation in simplifying complex calculations.
Practical Applications: Where is this Formula Used?
The formula for the perimeter of a regular polygon finds applications in diverse fields:
-
Architecture and Engineering: Calculating the amount of materials needed for fencing, building foundations, or designing structures with regular polygonal shapes. This includes everything from simple garden designs to complex constructions.
-
Cartography and Surveying: Determining distances and boundaries, especially in areas with regular polygonal features.
-
Computer Graphics and Game Development: Creating realistic simulations and games that often involve geometric objects, including regular polygons.
-
Packaging and Manufacturing: Designing containers and products with regular polygonal shapes. Optimization of packaging often relies on perimeter calculations.
-
Art and Design: Creating visually appealing designs and patterns based on the properties of regular polygons.
Examples: Calculating the Perimeter of Different Regular Polygons
Let's work through a few examples to solidify your understanding:
Example 1: Equilateral Triangle
An equilateral triangle has 3 sides, each measuring 5 cm. What is its perimeter?
- n = 3
- s = 5 cm
- Perimeter = n * s = 3 * 5 cm = 15 cm
Example 2: Square
A square has 4 sides, each measuring 8 inches. What is its perimeter?
- n = 4
- s = 8 inches
- Perimeter = n * s = 4 * 8 inches = 32 inches
Example 3: Regular Hexagon
A regular hexagon has 6 sides, each measuring 2.5 meters. What is its perimeter?
- n = 6
- s = 2.5 meters
- Perimeter = n * s = 6 * 2.5 meters = 15 meters
Example 4: Regular Octagon
A regular octagon has 8 sides, each measuring 3.2 feet. What is its perimeter?
- n = 8
- s = 3.2 feet
- Perimeter = n * s = 8 * 3.2 feet = 25.6 feet
Beyond the Basic Formula: Calculating Side Length from Perimeter
Often, you might know the perimeter and the number of sides but need to find the side length. The formula can be easily rearranged to solve for 's':
s = Perimeter / n
For instance, if a regular pentagon has a perimeter of 30 cm, then each side length is:
s = 30 cm / 5 = 6 cm
Advanced Concepts: Relating Perimeter to Apothem and Area
The perimeter of a regular polygon is closely related to its apothem and area. The apothem is the distance from the center of the polygon to the midpoint of any side. This relationship becomes particularly useful in calculating the area of the polygon:
Area = (Perimeter * Apothem) / 2
Understanding this connection enables the calculation of area given the perimeter and apothem, or vice-versa. This is essential for solving more complex geometric problems.
Dealing with Irregular Polygons: A Brief Overview
While this guide focuses on regular polygons, it's crucial to understand that the simple perimeter formula (n * s) doesn't apply to irregular polygons. Irregular polygons have sides of different lengths and angles. For irregular polygons, the perimeter is calculated by summing the lengths of all individual sides. This requires measuring each side separately, making the calculation more tedious but still fundamentally based on adding up the lengths of all the sides.
Conclusion: Mastering the Perimeter of Regular Polygons
The formula for the perimeter of a regular polygon – Perimeter = n * s – is a foundational concept with far-reaching applications. Understanding its derivation, its practical uses, and its relationship to other geometric properties empowers you to solve a wide range of problems in various fields. This guide has provided a comprehensive exploration of the topic, catering to different skill levels and offering ample examples to reinforce your understanding. Remember to always clearly define 'n' (number of sides) and 's' (side length) before applying the formula to ensure accuracy in your calculations. With this knowledge, you're well-equipped to tackle any perimeter problem involving regular polygons with confidence.
Latest Posts
Latest Posts
-
Why Is Water Considered To Be A Renewable Resource
Mar 30, 2025
-
Find The Area Under The Curve Calculator
Mar 30, 2025
-
Is Butter Melting A Physical Change
Mar 30, 2025
-
How Many Cm Are In 12 Inches
Mar 30, 2025
-
What Metals Are The Most Reactive
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Formula For Perimeter Of Regular Polygon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
