Find The Prime Factorization Of 75
Juapaving
Apr 04, 2025 · 5 min read
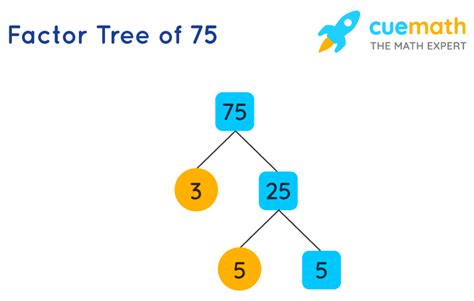
Table of Contents
Finding the Prime Factorization of 75: A Comprehensive Guide
Finding the prime factorization of a number is a fundamental concept in number theory. It involves expressing a number as a product of its prime factors – numbers that are only divisible by 1 and themselves. This process is crucial for various mathematical operations and applications, from simplifying fractions to understanding complex number relationships. This article will delve into the method of finding the prime factorization of 75, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also discuss broader applications of prime factorization and its significance in more advanced mathematical contexts.
Understanding Prime Numbers and Factorization
Before embarking on the prime factorization of 75, let's solidify our understanding of key terms.
What is a Prime Number?
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. The number 1 is neither prime nor composite.
What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of finding the prime numbers that, when multiplied together, equal the original number. Every composite number (a number greater than 1 that is not prime) can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factorization of 75: A Step-by-Step Approach
Now, let's systematically find the prime factorization of 75. There are several methods to achieve this; we'll use the method of successive division by prime numbers.
-
Start with the smallest prime number: The smallest prime number is 2. However, 75 is an odd number, so it's not divisible by 2.
-
Move to the next prime number: The next prime number is 3. We check if 75 is divisible by 3. The rule of divisibility for 3 states that a number is divisible by 3 if the sum of its digits is divisible by 3. In this case, 7 + 5 = 12, which is divisible by 3. Therefore, 75 is divisible by 3.
-
Perform the division: 75 ÷ 3 = 25. So we can write 75 as 3 × 25.
-
Continue with the quotient: Now we need to find the prime factorization of 25. 25 is not divisible by 3. The next prime number is 5. 25 is divisible by 5 (25 ÷ 5 = 5).
-
Final Prime Factors: We have now expressed 25 as 5 × 5. Since 5 is a prime number, we have reached the end of our factorization.
-
Putting it all together: Combining the results from steps 3 and 5, we have the prime factorization of 75 as 3 × 5 × 5, or 3 × 5².
Alternative Methods for Prime Factorization
While the method of successive division is straightforward, other methods can be used to find the prime factorization of a number, especially for larger numbers.
Factor Tree Method
The factor tree method is a visual approach. You start by branching out the number into any two factors. You then continue branching out each factor until you only have prime numbers at the ends of the branches. For 75, a factor tree might look like this:
75
/ \
3 25
/ \
5 5
This clearly shows the prime factorization as 3 × 5 × 5.
Division Method using Prime Numbers
This method systematically divides the number by prime numbers until only 1 remains.
| Number | Prime Divisor | Quotient |
|---|---|---|
| 75 | 3 | 25 |
| 25 | 5 | 5 |
| 5 | 5 | 1 |
The prime divisors used (3, 5, 5) represent the prime factorization: 3 × 5 × 5.
Applications of Prime Factorization
Prime factorization is not merely an academic exercise; it has numerous applications in various areas of mathematics and beyond:
Simplifying Fractions
Prime factorization simplifies the process of simplifying fractions. By finding the prime factors of the numerator and denominator, we can identify common factors and cancel them out, reducing the fraction to its simplest form.
For example, consider the fraction 75/100. The prime factorization of 75 is 3 × 5², and the prime factorization of 100 is 2² × 5². Therefore, 75/100 simplifies to (3 × 5²) / (2² × 5²) = 3/4.
Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization is essential for calculating the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
For example, let's find the GCD and LCM of 75 and 100.
- Prime factorization of 75: 3 × 5²
- Prime factorization of 100: 2² × 5²
The GCD is found by taking the lowest power of common prime factors: 5². Therefore, GCD(75, 100) = 25.
The LCM is found by taking the highest power of all prime factors present: 2² × 3 × 5². Therefore, LCM(75, 100) = 300.
Cryptography
Prime numbers play a vital role in modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime factors. The larger the prime numbers used, the more secure the encryption becomes.
Modular Arithmetic and Number Theory
Prime factorization is fundamental to numerous concepts in modular arithmetic and number theory, such as Fermat's Little Theorem and Euler's totient theorem. These theorems are essential for understanding the behavior of numbers under modular operations.
Conclusion: The Significance of Prime Factorization
The prime factorization of 75, as we've seen, is 3 × 5². This seemingly simple calculation underpins a wealth of mathematical concepts and applications. Understanding prime factorization is not just about finding the prime factors of a number; it's about grasping a foundational principle that permeates various branches of mathematics and even extends into the realm of computer science and cryptography. Its importance lies in its ability to simplify complex calculations, provide insights into number relationships, and serve as a building block for more advanced mathematical theories and applications. Mastering this concept opens doors to a deeper understanding of the fascinating world of numbers.
Latest Posts
Latest Posts
-
Ions With A Positive Charge Are Called
Apr 05, 2025
-
5 Letter Word Starts With A P
Apr 05, 2025
-
Anaerobic Respiration Takes Place In The
Apr 05, 2025
-
Can Dielectric Constant Be Less Than 1
Apr 05, 2025
-
1 1 4 As A Percent
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Prime Factorization Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
