Find The Prime Factorization Of 100
Juapaving
Apr 03, 2025 · 5 min read
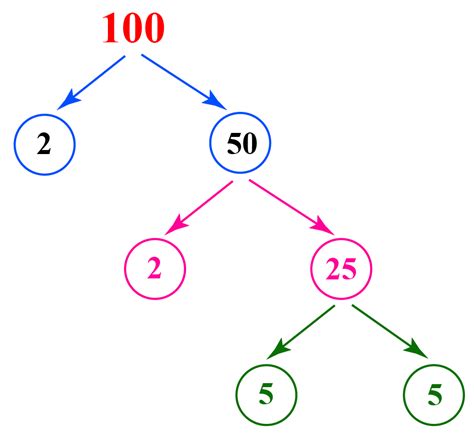
Table of Contents
Finding the Prime Factorization of 100: A Comprehensive Guide
Finding the prime factorization of a number is a fundamental concept in number theory. It involves expressing a number as a product of its prime factors – numbers that are only divisible by 1 and themselves. This seemingly simple process is crucial for understanding various mathematical concepts and has applications in cryptography, computer science, and beyond. This article delves into the prime factorization of 100, providing a detailed explanation of the method and exploring its broader significance.
Understanding Prime Numbers and Factorization
Before we tackle the prime factorization of 100, let's solidify our understanding of the key terms:
-
Prime Numbers: These are whole numbers greater than 1 that are only divisible by 1 and themselves. The first few prime numbers are 2, 3, 5, 7, 11, and so on. A crucial point is that 1 is not considered a prime number.
-
Prime Factorization: This is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Each composite number has a unique prime factorization, regardless of the order of the factors. This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic.
-
Composite Numbers: These are whole numbers greater than 1 that are not prime. They can be expressed as a product of two or more prime numbers.
Methods for Finding Prime Factorization
Several methods can be used to find the prime factorization of a number. Let's explore a few, focusing on their application to finding the prime factorization of 100.
1. Factor Tree Method
The factor tree method is a visual and intuitive approach, particularly useful for smaller numbers like 100. We start by breaking down the number into any two factors, and then continue breaking down those factors until we only have prime numbers left.
Let's illustrate this with 100:
-
Start with 100. We can express it as 10 x 10.
-
Now, break down each 10: 10 = 2 x 5
-
Since 2 and 5 are both prime numbers, we've reached the end of our factorization.
Therefore, the prime factorization of 100 using the factor tree method is 2 x 2 x 5 x 5, which can also be written as 2² x 5².
2. Repeated Division Method
This method involves repeatedly dividing the number by the smallest prime number that divides it evenly. We continue this process until the quotient is 1.
Let's apply this to 100:
-
Divide 100 by 2 (the smallest prime number): 100 ÷ 2 = 50
-
Divide 50 by 2: 50 ÷ 2 = 25
-
25 is not divisible by 2, but it is divisible by 5: 25 ÷ 5 = 5
-
Divide 5 by 5: 5 ÷ 5 = 1
We have reached 1, so the process is complete. The prime factors we used are 2, 2, 5, and 5. Thus, the prime factorization of 100 is 2² x 5².
3. Using Known Factor Pairs
For numbers with easily identifiable factors, this method can be quite efficient. We start by recognizing pairs of factors and then break those factors down into primes.
For 100, we can immediately see that 10 x 10 = 100. Then, we know that 10 = 2 x 5. Therefore, 100 = 2 x 5 x 2 x 5 = 2² x 5².
The Significance of Prime Factorization of 100
While finding the prime factorization of 100 might seem like a simple exercise, it highlights several important mathematical concepts:
-
Uniqueness: The prime factorization of 100 (2² x 5²) is unique. No other combination of prime numbers will multiply to give 100. This is a fundamental property guaranteed by the Fundamental Theorem of Arithmetic.
-
Greatest Common Divisor (GCD): Prime factorization is crucial for finding the greatest common divisor of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder. For example, to find the GCD of 100 and another number, we can use their prime factorizations to identify common factors.
-
Least Common Multiple (LCM): Similarly, prime factorization helps determine the least common multiple of two or more numbers. The LCM is the smallest number that is a multiple of all the given numbers.
-
Applications in Cryptography: Prime factorization plays a vital role in modern cryptography, particularly in RSA encryption. The security of RSA relies on the difficulty of factoring large numbers into their prime components.
Beyond 100: Extending the Concepts
The methods used to find the prime factorization of 100 can be applied to any whole number. However, as numbers get larger, the process can become more complex. For very large numbers, sophisticated algorithms are employed. These algorithms are optimized for efficiency and are essential in computational number theory and cryptography.
Practical Applications and Real-World Examples
The prime factorization isn't just a theoretical concept; it has numerous practical applications across various fields:
-
Coding and Computer Science: Understanding prime factorization is important in algorithms related to cryptography, data compression, and random number generation. Efficient factorization algorithms are crucial for the security of many online systems.
-
Mathematics and Number Theory: Prime factorization is fundamental to many areas of number theory, including modular arithmetic, Diophantine equations, and the study of prime number distribution.
-
Chemistry and Physics: Prime factorization concepts can be surprisingly relevant in understanding molecular structures and chemical reactions.
-
Engineering and Design: Certain engineering problems might require optimization based on prime factorization principles.
Conclusion: The Enduring Importance of Prime Factorization
Finding the prime factorization of 100 – 2² x 5² – is more than just a simple mathematical exercise. It’s a gateway to understanding fundamental concepts in number theory, which have far-reaching applications in various fields. From the security of online transactions to the development of sophisticated algorithms, prime factorization remains a cornerstone of modern mathematics and computer science. Mastering this concept provides a strong foundation for further exploration in these exciting and rapidly evolving disciplines. The seemingly simple act of breaking down a number into its prime components reveals a depth and complexity that continues to fascinate mathematicians and computer scientists alike. As we continue to explore the mysteries of numbers, the prime factorization remains a powerful tool in our arsenal.
Latest Posts
Latest Posts
-
5 Letter Word Starts With Vi
Apr 04, 2025
-
What Is The Symbol For Calcium
Apr 04, 2025
-
Diagonal Cross Section Of A Pyramid Example
Apr 04, 2025
-
What Is The Lowest Common Multiple Of 8 And 12
Apr 04, 2025
-
Data And Information Are Interchangeable Terms True Or False
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Prime Factorization Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
