Diagonal Cross Section Of A Pyramid Example
Juapaving
Apr 04, 2025 · 6 min read
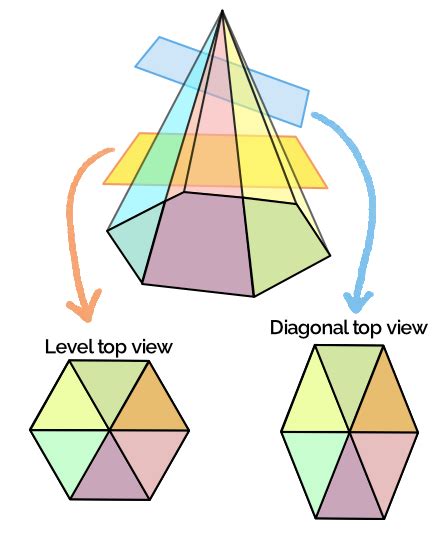
Table of Contents
Diagonal Cross Section of a Pyramid: A Comprehensive Guide
Understanding the geometry of pyramids, especially their cross-sections, is crucial in various fields like architecture, engineering, and even game development. While many focus on simpler cross-sections, the diagonal cross-section presents a unique challenge and offers fascinating insights into the pyramid's internal structure. This comprehensive guide will explore the concept of diagonal cross-sections in pyramids, providing a detailed explanation, examples, and practical applications.
What is a Diagonal Cross-Section?
A cross-section is essentially a two-dimensional (2D) shape created when a three-dimensional (3D) object is sliced through. A diagonal cross-section specifically involves slicing the 3D object along a plane that intersects the object's diagonal. In the context of a pyramid, this means cutting through the pyramid in a way that doesn't follow any of the existing edges or faces, but rather creates a new polygon intersecting multiple sides. This creates a unique geometric shape dependent on the pyramid's dimensions and the angle of the cut.
The complexity of the resulting shape depends on the type of pyramid: a regular square pyramid will produce distinctly different results than an irregular triangular pyramid.
Types of Pyramids and their Diagonal Cross-Sections
Before diving into specific examples, let's categorize the types of pyramids we'll consider:
1. Regular Square Pyramid:
A regular square pyramid has a square base and four congruent triangular faces. Its apex (top point) lies directly above the center of the square base. A diagonal cross-section of a regular square pyramid can take various forms, depending on the plane's orientation.
-
Symmetrical Cuts: If the slicing plane passes through opposite vertices of the base and the apex, the cross-section will be an isosceles triangle. The base of the triangle is a diagonal of the square base of the pyramid, and the other two sides are segments of the pyramid's lateral edges.
-
Asymmetrical Cuts: A cut that doesn't pass through the apex and opposite base vertices results in more complex shapes. This might be a trapezoid or even a quadrilateral with no parallel sides, depending on the plane's angle.
2. Rectangular Pyramid:
A rectangular pyramid has a rectangular base and four triangular faces. Its apex can be directly above the center of the rectangle (making it a right rectangular pyramid) or offset (an oblique rectangular pyramid). Diagonal cross-sections in these pyramids can be even more varied than in square pyramids. They will frequently result in trapezoids, quadrilaterals, or even pentagons depending on how it intersects the pyramid’s faces. The lack of symmetry inherent in rectangular bases increases the variability in the shape of the diagonal cross-section.
3. Triangular Pyramid (Tetrahedron):
A triangular pyramid, also known as a tetrahedron, has a triangular base and three other triangular faces. While a diagonal cross-section can be created here, it is important to note that a simple diagonal cut might just result in another triangle — a smaller version of one of the original faces or a completely different triangle. More complex cuts might create quadrilaterals.
Examples of Diagonal Cross-Sections
Let's illustrate with specific examples:
Example 1: Isosceles Triangle Cross-Section of a Square Pyramid
Imagine a regular square pyramid with a base side length of 8 units and a height of 6 units. If we slice through the pyramid such that the plane passes through opposite vertices of the base and the apex, the resulting diagonal cross-section will be an isosceles triangle.
- Base of the Triangle: The diagonal of the square base, calculated using the Pythagorean theorem: √(8² + 8²) = √128 ≈ 11.31 units.
- Height of the Triangle: This will be equal to the height of the pyramid itself, which is 6 units.
- Two Equal Sides of the Triangle: These sides will be equal in length, and their length can be calculated using the Pythagorean theorem, involving the height of the pyramid and half the diagonal of the base.
Example 2: Trapezoidal Cross-Section of a Rectangular Pyramid
Consider a rectangular pyramid with base dimensions of 6 units and 10 units, and a height of 8 units. A diagonal cross-section that doesn’t pass through the apex and base vertices will likely result in a trapezoid. The precise dimensions of this trapezoid will depend heavily on the specific orientation of the cutting plane.
Example 3: Complex Quadrilateral Cross-Section
For irregular pyramids or oblique pyramids, the resulting diagonal cross-sections can be quite complex, often resulting in irregular quadrilaterals with no easily definable characteristics.
Calculating Area and Volume of Diagonal Cross-Sections
Calculating the area of a diagonal cross-section can be challenging, as the shape is often irregular. If the cross-section is a simple shape like a triangle or trapezoid, standard geometric formulas can be used. However, for more complex shapes, methods like dividing the shape into smaller triangles or using numerical integration might be necessary.
Determining the volume of the pyramid after being sectioned is a more complex problem as the overall volume has been altered. The volume calculations require a precise understanding of the shape and dimensions of the removed section and the remaining portion.
Applications of Diagonal Cross-Sections
Understanding diagonal cross-sections has several practical applications:
- Architecture: Designing intricate roof structures, analyzing stress distribution in buildings, or optimizing material usage in construction.
- Engineering: Analyzing structural stability of bridges and other constructions.
- Mining: Determining the quantity of ore in a pyramidal ore deposit.
- Computer Graphics: Creating realistic 3D models of pyramids and other objects, generating textures and shading.
- Game Development: Building accurate game environments and realistic physics simulation.
Advanced Considerations
- Oblique Pyramids: Dealing with oblique pyramids drastically increases the difficulty of calculating cross-sectional areas and volumes. The lack of symmetry complicates the geometric analysis, often requiring advanced mathematical techniques like vector calculus.
- Multiple Cross-Sections: Analyzing the interplay of multiple diagonal cross-sections or considering cross-sections alongside other types of sections (e.g., parallel to the base) can unveil intricate internal structural relationships.
- 3D Modeling Software: Utilizing 3D modeling software can be an invaluable tool for visualizing and analyzing diagonal cross-sections. This software allows for dynamic manipulation of the cutting plane, generating accurate depictions of the resulting shapes and facilitating measurements.
Conclusion
The diagonal cross-section of a pyramid is a fascinating geometric concept with far-reaching implications. While the resulting shapes can vary greatly based on the pyramid's type and the orientation of the cutting plane, understanding these concepts opens up opportunities in various fields, from design and engineering to computer graphics and game development. By mastering the principles outlined in this guide, you can effectively analyze, visualize, and calculate the properties of these complex cross-sections. Further exploration into advanced techniques and software tools can significantly enhance your ability to tackle intricate geometric challenges. Remember to always visualize the process; a clear understanding of the three-dimensional geometry is paramount in achieving accurate results.
Latest Posts
Latest Posts
-
11 Cm Is How Many Inches
Apr 04, 2025
-
How Tall Is 30 Inches In Feet
Apr 04, 2025
-
The Speed Of Light In A Vacuum Is
Apr 04, 2025
-
What Is The Largest Animal On Land
Apr 04, 2025
-
Find The Prime Factorization Of 75
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Diagonal Cross Section Of A Pyramid Example . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
