Find The Mean Of First Six Odd Numbers
Juapaving
May 09, 2025 · 4 min read
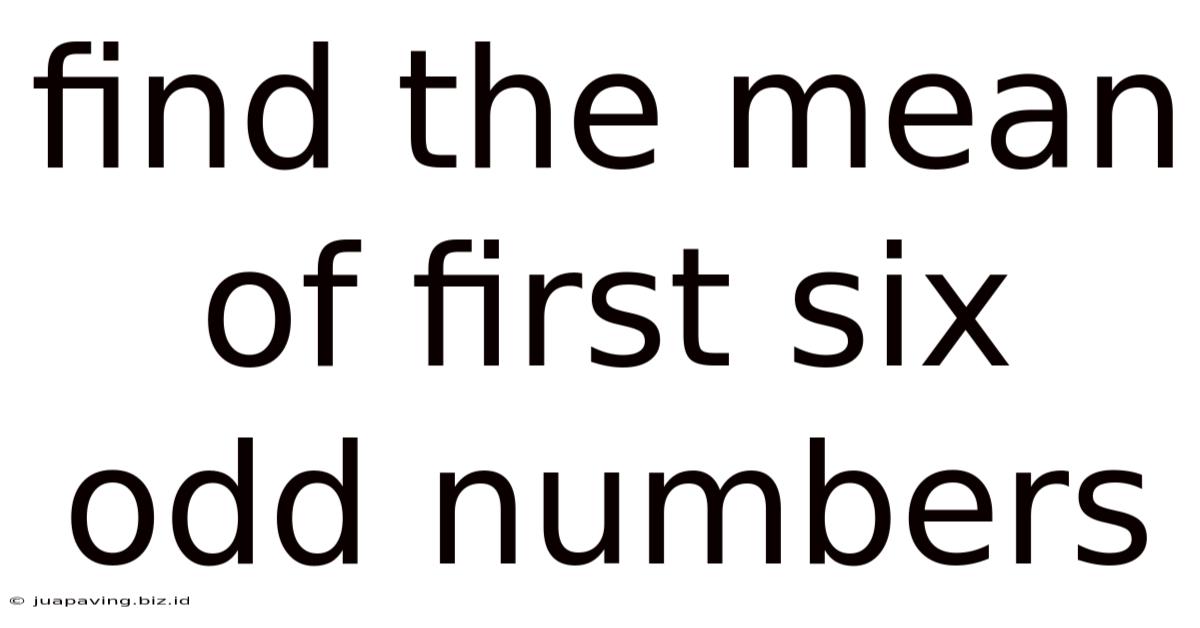
Table of Contents
Find the Mean of the First Six Odd Numbers: A Comprehensive Guide
Finding the mean (average) of a set of numbers is a fundamental concept in mathematics and statistics. This seemingly simple task—calculating the mean of the first six odd numbers—provides a great opportunity to explore various approaches and delve into related mathematical concepts. This comprehensive guide will not only solve the problem but also illuminate the underlying principles and offer broader insights into mean calculations and number sequences.
Understanding the Mean
Before diving into the specifics of our problem, let's solidify our understanding of the mean. The mean, or average, is a measure of central tendency. It represents the central value of a dataset. To calculate the mean, we sum all the numbers in the dataset and then divide by the total number of values. The formula is:
Mean = (Sum of all numbers) / (Total number of values)
Identifying the First Six Odd Numbers
The first step in our problem is to identify the first six odd numbers. Odd numbers are whole numbers that are not divisible by 2. The sequence begins:
1, 3, 5, 7, 9, 11
These are the numbers we will use to calculate the mean.
Method 1: Direct Calculation
The most straightforward method involves directly applying the mean formula:
- Sum the numbers: 1 + 3 + 5 + 7 + 9 + 11 = 36
- Count the numbers: There are 6 numbers in the set.
- Calculate the mean: 36 / 6 = 6
Therefore, the mean of the first six odd numbers is 6.
Method 2: Arithmetic Series
The first six odd numbers form an arithmetic series. An arithmetic series is a sequence where the difference between consecutive terms remains constant. In this case, the common difference is 2. Understanding this allows us to use a more efficient formula to calculate the sum:
Sum of an arithmetic series = (n/2) * [2a + (n-1)d]
Where:
- n is the number of terms (in our case, 6)
- a is the first term (1)
- d is the common difference (2)
Let's plug in the values:
Sum = (6/2) * [2(1) + (6-1)2] = 3 * [2 + 10] = 3 * 12 = 36
Again, dividing the sum (36) by the number of terms (6) gives us a mean of 6.
Method 3: Visual Representation and Pattern Recognition
Visualizing the data can often lead to insightful pattern recognition. Let's arrange the numbers in a line graph:
* * * * * *
1 3 5 7 9 11
Notice the symmetry around the middle value. The numbers are equally spaced, and the average will always be the middle value or the average of the two middle values in an even-numbered set. In this case, the middle value is exactly 6.
Extending the Concept: The Mean of the First 'n' Odd Numbers
We can generalize our findings to determine the mean of the first 'n' odd numbers. The sum of the first 'n' odd numbers is always equal to n². This can be proven mathematically using mathematical induction or through the formula for the sum of an arithmetic series.
Therefore, the mean of the first 'n' odd numbers is:
Mean = n²/n = n
This elegantly demonstrates that the mean of the first 'n' odd numbers is simply 'n'. For example, the mean of the first 10 odd numbers is 10, the mean of the first 100 odd numbers is 100, and so on.
Connecting to Other Mathematical Concepts
This seemingly simple problem connects to several other important mathematical concepts:
- Sequences and Series: The problem showcases arithmetic sequences and their properties, offering a foundation for understanding more complex sequences like geometric sequences and Fibonacci sequences.
- Summation Notation: The problem can be expressed using summation notation (Σ), providing a concise and powerful way to represent the sum of a series.
- Mathematical Induction: The proof that the sum of the first n odd numbers is n² often utilizes mathematical induction, a fundamental proof technique in mathematics.
Real-World Applications
While this specific problem might seem abstract, the concept of calculating means has extensive real-world applications:
- Statistics: Calculating averages is crucial in statistical analysis for everything from analyzing test scores to understanding economic indicators.
- Data Analysis: Mean calculation is a cornerstone of data analysis across diverse fields, including finance, engineering, and healthcare.
- Probability: The concept of average values is fundamental in probability theory, helping us to understand expected values and distributions.
Further Exploration
To further solidify your understanding, consider the following:
- Calculate the mean of the first ten odd numbers using different methods.
- Explore the mean of the first 'n' even numbers. (Hint: The sum of the first 'n' even numbers is n(n+1).)
- Investigate the mean of other types of number sequences. (Consider geometric sequences or Fibonacci sequences.)
Conclusion
Finding the mean of the first six odd numbers, while seemingly simple, provides a valuable springboard to explore fundamental mathematical concepts like arithmetic series, summation notation, and the broader applications of calculating means in various fields. By understanding the methods and underlying principles, you not only solve the problem but also gain a deeper appreciation for the power and versatility of mathematical tools. This understanding forms a strong base for tackling more complex mathematical challenges and real-world problems. Remember that consistent practice and exploration of related concepts are key to mastering these essential skills.
Latest Posts
Latest Posts
-
Calcium Oxide Carbon Dioxide Calcium Carbonate
May 11, 2025
-
How Long Is 75 Inches In Feet
May 11, 2025
-
Words To Describe A Childs Character
May 11, 2025
-
How Are Deserts And Tundras Alike
May 11, 2025
-
What Is The Percentage Of 2 Out Of 8
May 11, 2025
Related Post
Thank you for visiting our website which covers about Find The Mean Of First Six Odd Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.