What Is The Percentage Of 2 Out Of 8
Juapaving
May 11, 2025 · 5 min read
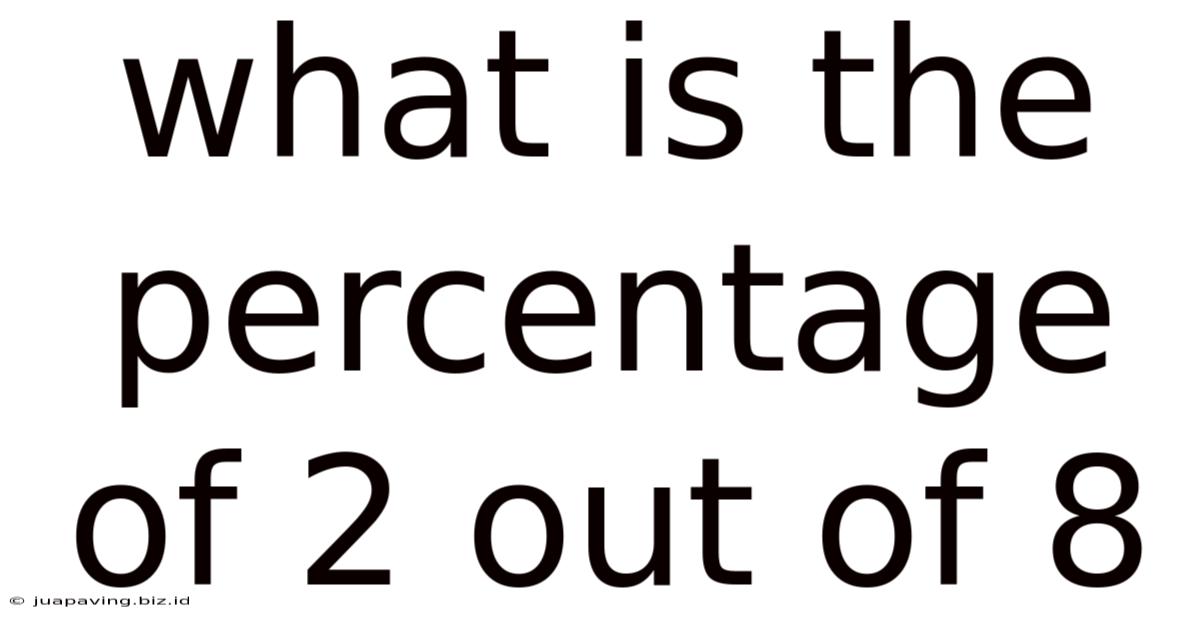
Table of Contents
What is the Percentage of 2 out of 8? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with far-reaching applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the seemingly simple question, "What is the percentage of 2 out of 8?", and then expand upon the broader concepts of percentages, their calculation, and their diverse uses across various fields.
Calculating the Percentage: A Step-by-Step Guide
The core concept revolves around expressing a fraction as a portion of 100. To find the percentage of 2 out of 8, we follow these steps:
-
Form a fraction: Express the given numbers as a fraction: 2/8. This represents 2 parts out of a total of 8 parts.
-
Simplify the fraction (optional but recommended): Dividing both the numerator (2) and the denominator (8) by their greatest common divisor (2), we simplify the fraction to 1/4. This makes the next step easier.
-
Convert the fraction to a decimal: Divide the numerator by the denominator: 1 ÷ 4 = 0.25
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.25 x 100 = 25%.
Therefore, 2 out of 8 is 25%.
Beyond the Basics: Understanding Percentage Concepts
While calculating 25% from 2 out of 8 is straightforward, a deeper understanding of percentages is crucial for their effective application. Let's explore some key concepts:
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). It's a universally understood and convenient way to compare proportions and ratios.
Percentage vs. Fraction vs. Decimal
These three representations are interchangeable:
- Fraction: Represents a part of a whole using a numerator (top number) and a denominator (bottom number). Example: 1/4
- Decimal: Represents a number using the base-10 system. Example: 0.25
- Percentage: Represents a fraction or decimal as a portion of 100. Example: 25%
Understanding their interrelationships allows for easy conversions between them.
Applications of Percentages: Real-world Examples
Percentages are ubiquitous in various aspects of life:
- Finance: Calculating interest rates, discounts, taxes, profit margins, investment returns, inflation rates.
- Statistics: Representing data in charts and graphs, conducting statistical analysis, calculating probabilities.
- Science: Expressing concentrations of solutions, analyzing experimental results, calculating error margins.
- Everyday life: Understanding sale prices, calculating tips, interpreting survey results, comparing different products.
Advanced Percentage Calculations and Problem-Solving
Let's explore more complex scenarios involving percentages:
Finding the Percentage of a Number
This involves multiplying the number by the percentage (expressed as a decimal). For example, to find 25% of 120, we calculate: 0.25 x 120 = 30.
Finding a Number Given its Percentage
This involves using the following formula: Number = (Percentage/100) x Whole. For instance, if 25% of a number is 30, we can find the number by solving: 30 = (25/100) x Whole. This solves to a whole of 120.
Percentage Increase and Decrease
These calculations are frequently used to track changes over time:
- Percentage increase: [(New Value - Old Value) / Old Value] x 100
- Percentage decrease: [(Old Value - New Value) / Old Value] x 100
For example, if a price increases from $100 to $120, the percentage increase is [(120-100)/100] x 100 = 20%.
Percentage Points vs. Percentage Change
It's crucial to differentiate between these two:
- Percentage points: The difference between two percentages. For example, if interest rates rise from 2% to 5%, the increase is 3 percentage points.
- Percentage change: The relative change expressed as a percentage. In the interest rate example, the percentage change is [(5-2)/2] x 100 = 150%.
Error Analysis and Accuracy in Percentage Calculations
Inaccuracy can stem from various sources, such as:
- Rounding errors: Rounding intermediate calculations can lead to slight discrepancies in the final result.
- Data entry errors: Incorrect input data will inevitably produce wrong results.
- Misinterpretation of percentages: Confusing percentage points with percentage change can lead to flawed conclusions.
Always strive for accuracy and use appropriate rounding strategies. Double-checking calculations is crucial, particularly in critical applications.
Applications of Percentages in Different Fields
Let's examine how percentages are used in specific domains:
Finance: A Cornerstone of Financial Literacy
Percentages are fundamental in personal finance and investment analysis. Understanding interest rates, annual percentage yields (APYs), and compound interest are crucial for making informed financial decisions. Analyzing investment returns and calculating loan repayments also relies heavily on percentage calculations.
Statistics: Unveiling Data Trends and Patterns
Percentages facilitate data interpretation and comparison. In surveys and polls, percentages represent the proportion of respondents who chose a particular answer. Statistical analysis uses percentages to express probabilities, confidence intervals, and other key metrics. Graphical representations like pie charts utilize percentages to visualize data proportions effectively.
Healthcare: Measuring Health Outcomes and Risks
Percentages play a significant role in healthcare. Mortality rates, success rates of medical procedures, disease prevalence, and risk factors are often expressed as percentages. These statistics help in assessing healthcare outcomes, identifying high-risk groups, and informing public health policies.
Business and Marketing: Analyzing Sales, Growth, and Market Share
Businesses use percentages to track sales growth, calculate market share, analyze profit margins, and assess the return on investment (ROI) of various marketing campaigns. Understanding these metrics is crucial for strategic decision-making and business growth.
Education: Evaluating Student Performance and Academic Progress
In education, percentages are used to grade student performance, assess the effectiveness of teaching methods, and evaluate the progress of students. Calculating grade point averages (GPAs) also relies on percentage calculations.
Conclusion: The Enduring Significance of Percentages
The seemingly simple calculation of "What is the percentage of 2 out of 8?" opens a gateway to the vast world of percentage applications. Understanding percentages is an essential skill applicable across diverse fields, from managing personal finances and analyzing statistical data to understanding business trends and assessing healthcare outcomes. Mastering percentage calculations and comprehending their underlying principles empowers individuals to make informed decisions and navigate the complexities of the modern world with confidence. This knowledge facilitates informed financial decisions, data-driven insights, and a deeper understanding of the world around us. The significance of percentages extends far beyond simple mathematical computations; it forms a cornerstone of numerical literacy essential for success in numerous aspects of life.
Latest Posts
Latest Posts
-
1 1 4 As An Improper Fraction
May 12, 2025
-
Find The Equivalent Fraction Of 15 35 With Denominator 7
May 12, 2025
-
Is Digesting Food A Physical Change
May 12, 2025
-
Difference Between Combinational Circuit And Sequential Circuit
May 12, 2025
-
30 45 60 Sin Cos Tan
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 2 Out Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.