What Is The Prime Factors Of 150
Juapaving
Apr 02, 2025 · 5 min read
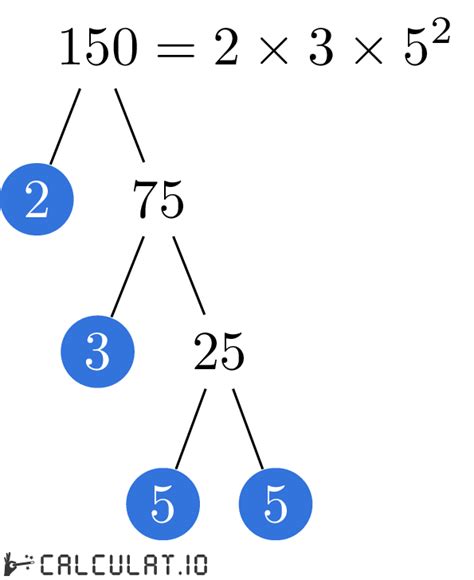
Table of Contents
What are the Prime Factors of 150? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but it’s a fundamental concept with far-reaching applications in number theory, cryptography, and even computer science. This article will not only answer the question "What are the prime factors of 150?" but will also explore the underlying principles of prime factorization, provide various methods for solving such problems, and discuss the significance of prime numbers in broader mathematical contexts.
Understanding Prime Numbers and Prime Factorization
Before diving into the prime factorization of 150, let's solidify our understanding of the key terms:
-
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. The number 1 is not considered a prime number.
-
Composite Number: A composite number is a positive integer that has at least one positive divisor other than 1 and itself. In essence, it's a number that can be factored into smaller positive integers. Examples include 4, 6, 9, 10, and so on.
-
Prime Factorization (or Prime Decomposition): This is the process of finding the prime numbers that, when multiplied together, give the original number. Every composite number can be expressed as a unique product of prime numbers (Fundamental Theorem of Arithmetic).
Finding the Prime Factors of 150: Method 1 – The Factor Tree
One of the most common and visually intuitive methods for finding prime factors is using a factor tree. Here's how it works for 150:
-
Start with the number: Begin with the number 150 at the top of your tree.
-
Find two factors: Find any two factors of 150. A simple starting point is 2 and 75 (since 150 is an even number, it's divisible by 2).
-
Branch out: Draw two branches from 150, one leading to 2 and the other to 75.
-
Continue factoring: The number 2 is a prime number, so we stop branching from it. However, 75 is composite. We can factor 75 into 3 and 25. Add branches from 75 to 3 and 25.
-
Keep going until all factors are prime: 3 is prime, so we stop there. 25 is composite (5 x 5), so we further break it down into two 5s.
-
Identify the prime factors: Once all branches end in prime numbers, you've found the prime factors. In the case of 150, they are 2, 3, and 5 (with 5 appearing twice).
Therefore, the prime factorization of 150 is 2 x 3 x 5 x 5, or 2 x 3 x 5².
Finding the Prime Factors of 150: Method 2 – Repeated Division
This method is more systematic and particularly useful for larger numbers. It involves repeatedly dividing the number by the smallest prime number that divides it evenly until you reach 1.
-
Start with the number: Begin with 150.
-
Divide by the smallest prime factor: The smallest prime number that divides 150 is 2. 150 / 2 = 75.
-
Repeat: Now divide 75 by the smallest prime factor that divides it evenly. That's 3. 75 / 3 = 25.
-
Continue until you reach 1: The smallest prime factor of 25 is 5. 25 / 5 = 5. Finally, 5 / 5 = 1.
-
Identify the prime factors: The prime numbers used in the divisions are 2, 3, and 5 (with 5 appearing twice).
Again, this confirms that the prime factorization of 150 is 2 x 3 x 5².
The Significance of Prime Factorization
The seemingly simple process of prime factorization holds significant weight in various mathematical and computational fields:
1. Number Theory:
Prime factorization is fundamental to understanding the properties of numbers, including concepts like greatest common divisors (GCD), least common multiples (LCM), and modular arithmetic. These concepts are crucial in cryptography and coding theory.
2. Cryptography:
Many modern encryption algorithms rely on the difficulty of factoring very large numbers into their prime factors. The RSA algorithm, a widely used public-key cryptosystem, is a prime example. The security of RSA depends on the computational infeasibility of factoring extremely large composite numbers with hundreds or even thousands of digits.
3. Computer Science:
Prime factorization algorithms are used in various computer science applications, including:
- Hashing: Prime numbers are often used in hash table algorithms to minimize collisions.
- Random Number Generation: Prime numbers play a role in generating pseudo-random numbers used in simulations and other computational tasks.
- Error Correction Codes: Prime numbers are used in the design of error correction codes for data transmission and storage.
4. Mathematics Education:
Understanding prime factorization helps students develop a deeper understanding of number systems, algebraic concepts, and problem-solving skills. It bridges the gap between basic arithmetic and more advanced mathematical topics.
Beyond 150: Exploring Prime Factorization Techniques for Larger Numbers
While the factor tree and repeated division methods work well for smaller numbers like 150, they become less efficient for larger numbers. For very large composite numbers, specialized algorithms are necessary:
-
Trial Division: This involves testing divisibility by successively larger prime numbers. While simple, it becomes computationally expensive for large numbers.
-
Pollard's Rho Algorithm: A probabilistic algorithm that is more efficient than trial division for moderately sized numbers.
-
General Number Field Sieve (GNFS): The most efficient known algorithm for factoring very large numbers. It's used for breaking cryptographic systems that rely on the difficulty of factoring large numbers.
Conclusion: The Prime Factors of 150 and Beyond
We've conclusively shown that the prime factors of 150 are 2, 3, and 5 (with 5 appearing twice), expressed as 2 x 3 x 5². However, this exploration goes far beyond simply solving a single factorization problem. It highlights the fundamental importance of prime numbers and prime factorization in mathematics and computer science. Understanding these concepts provides a strong foundation for tackling more complex mathematical problems and appreciating the power of seemingly simple mathematical operations. The seemingly straightforward task of finding the prime factors of 150 opens a door to a fascinating world of mathematical exploration and its practical applications in our increasingly digital world.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Compound
Apr 03, 2025
-
What Is The Lcm Of 3 And 7
Apr 03, 2025
-
A Circle Is Continuously Rotated About Its Diameter
Apr 03, 2025
-
How Many Feet In 25 Meters
Apr 03, 2025
-
What Is The Most Common Gas In The Atmosphere
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factors Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
