Electric Field Due To Infinite Line Charge
Juapaving
Mar 26, 2025 · 6 min read
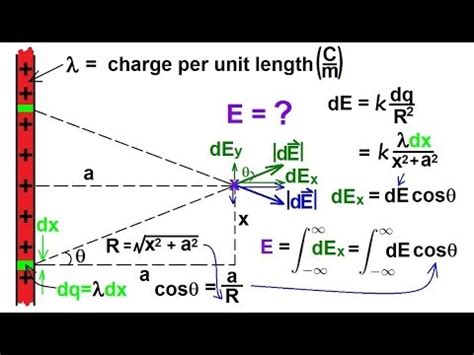
Table of Contents
Electric Field Due to an Infinite Line Charge: A Comprehensive Guide
Understanding the electric field generated by an infinite line charge is a fundamental concept in electromagnetism with wide-ranging applications. While a truly infinite line charge is a theoretical construct, it serves as an excellent approximation for many real-world scenarios involving long, thin charged conductors. This comprehensive guide will explore the derivation of the electric field, its characteristics, and its significance in various fields of physics and engineering.
Understanding the Concept
Before diving into the derivation, let's establish a clear understanding of the key concepts:
-
Electric Field: A region of space surrounding a charged object where a force is exerted on other charged objects. It's a vector quantity, possessing both magnitude and direction. The direction of the electric field at a point is defined as the direction of the force that would be experienced by a positive test charge placed at that point.
-
Line Charge Density (λ): This represents the amount of charge per unit length along the infinite line. It's expressed in Coulombs per meter (C/m). A uniformly charged line implies that λ is constant along the entire length.
-
Coulomb's Law: This fundamental law governs the electrostatic interaction between charged particles. It states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. This law forms the basis for calculating the electric field due to various charge distributions.
-
Gauss's Law: A powerful tool in electromagnetism, Gauss's law relates the flux of the electric field through a closed surface to the net charge enclosed within that surface. It simplifies the calculation of electric fields, especially for symmetrical charge distributions like the infinite line charge.
Derivation of the Electric Field using Gauss's Law
Gauss's Law provides the most elegant and efficient method for deriving the electric field due to an infinite line charge. Here's a step-by-step breakdown:
-
Choosing the Gaussian Surface: The key to successfully applying Gauss's Law is selecting an appropriate Gaussian surface—a closed surface through which the electric field flux is easily calculated. Due to the cylindrical symmetry of the infinite line charge, a cylindrical Gaussian surface is the optimal choice. This cylinder should have a radius 'r' and length 'L', with the line charge running along its axis.
-
Electric Field Symmetry: By symmetry, the electric field at any point on the cylindrical Gaussian surface must be radial and perpendicular to the line charge. This means the electric field lines are directed radially outwards (if the line charge is positive) or inwards (if negative).
-
Flux Calculation: The electric flux (Φ) through the Gaussian surface is given by the surface integral of the electric field (E) over the surface area (A). Due to the radial symmetry, the electric field is constant in magnitude on the curved surface of the cylinder and perpendicular to it. The flux through the circular ends of the cylinder is zero, as the electric field is parallel to these surfaces. Thus, the total flux is:
Φ = E * A<sub>curved</sub> = E * (2πrL)
-
Applying Gauss's Law: Gauss's Law states that the total flux through a closed surface is proportional to the enclosed charge (Q<sub>enc</sub>):
Φ = Q<sub>enc</sub> / ε₀
where ε₀ is the permittivity of free space (a constant).
-
Relating Charge and Line Charge Density: The enclosed charge within the Gaussian cylinder is simply the line charge density multiplied by the length of the cylinder:
Q<sub>enc</sub> = λL
-
Solving for the Electric Field: By equating the expressions for flux from steps 3 and 4, and substituting the expression for enclosed charge from step 5, we get:
E * (2πrL) = (λL) / ε₀
Solving for E, we obtain the magnitude of the electric field:
E = λ / (2πε₀r)
This equation reveals a crucial characteristic of the electric field due to an infinite line charge: it's inversely proportional to the distance (r) from the line charge. This means the field strength decreases as you move further away from the line.
Vector Form of the Electric Field
The equation derived above gives the magnitude of the electric field. To express it as a vector, we need to consider the direction. For a positive line charge, the electric field points radially outward from the line. Using the radial unit vector r̂, the vector form of the electric field is:
E = (λ / 2πε₀r) r̂
For a negative line charge, the direction would be reversed.
Applications and Significance
The concept of the electric field due to an infinite line charge finds applications in diverse areas:
1. Coaxial Cables:
Coaxial cables consist of a central conductor surrounded by a concentric outer conductor. The electric field between these conductors can be approximated using the infinite line charge model, which is crucial for understanding the cable's capacitance and signal transmission characteristics. The model simplifies the complex interactions and accurately predicts the field strength between the conductors.
2. Cylindrical Capacitors:
Similar to coaxial cables, cylindrical capacitors utilize two concentric cylindrical conductors to store charge. The electric field between the cylinders can be analyzed using the infinite line charge approximation, leading to a calculation of the capacitance of the device. This approximation yields accurate results if the length of the cylinders is significantly larger than their radii.
3. Charged Rods and Wires:
In many experimental setups, long thin rods or wires carry significant electric charge. The infinite line charge model provides a reasonably accurate approximation of the electric field near the center of these rods or wires, even though they are finite in length. The approximation's accuracy improves as the length of the conductor increases relative to the distance from the point of measurement.
4. Modeling Electrostatic Forces:
Understanding the electric field generated by an infinite line charge is crucial for calculating the electrostatic force on a charged particle placed in its vicinity. This knowledge finds application in various scenarios, from analyzing the motion of ions in an electric field to designing and modeling different electrostatic devices.
5. Electrostatic Shielding:
The concept of electric field distribution around an infinite line charge aids in understanding the effectiveness of cylindrical electrostatic shields. These shields are typically grounded and their ability to minimize external electric field interference can be analyzed using the infinite line charge approximation.
Limitations of the Infinite Line Charge Model
It's important to acknowledge that the infinite line charge is a simplification. Real-world conductors have finite lengths. The accuracy of the infinite line charge model decreases as the distance from the line becomes comparable to its length or when considering points near the ends of the conductor. At the ends of the finite line charge, the field lines diverge significantly from the radial pattern assumed in the model.
However, the model remains a valuable tool for understanding the fundamental principles of electrostatics and providing a good approximation in many situations involving long, thin conductors where the distance of interest is relatively small compared to the length of the conductor.
Conclusion
The electric field due to an infinite line charge is a cornerstone concept in electromagnetism. The derivation using Gauss's Law elegantly demonstrates the power of this theorem in simplifying calculations for symmetrical charge distributions. Understanding this model is crucial for tackling more complex problems in electrostatics and related fields like electrical engineering and physics. While recognizing the limitations of the infinite line charge approximation, its simplicity and usefulness make it an indispensable tool in the arsenal of any physics or engineering student or professional. Further exploration into the concept of finite line charges and more complex charge distributions builds upon this foundational understanding.
Latest Posts
Latest Posts
-
What Does A Million Dollars Look Like
Mar 29, 2025
-
Is Alcohol A Pure Substance Or A Mixture
Mar 29, 2025
-
Square Root Of 27 In Radical Form
Mar 29, 2025
-
Common Multiples Of 4 And 8
Mar 29, 2025
-
Are Planar And Angular Nodes The Same
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Due To Infinite Line Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
