What Are The Factors Of 117
Juapaving
Apr 06, 2025 · 5 min read
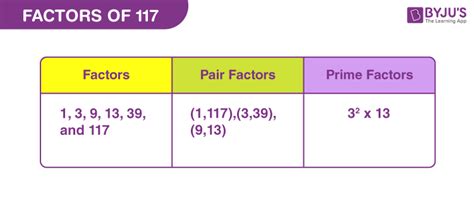
Table of Contents
What are the Factors of 117? A Deep Dive into Prime Factorization and Divisibility
Finding the factors of a number might seem like a simple arithmetic exercise, but understanding the process reveals fundamental concepts in number theory. This article delves deep into determining the factors of 117, exploring the methods involved, and expanding on related mathematical concepts like prime factorization and divisibility rules. We'll go beyond a simple list of factors to grasp the underlying principles, making this exploration beneficial for students and anyone interested in strengthening their mathematical understanding.
Understanding Factors and Divisibility
Before we tackle the specific case of 117, let's establish a clear understanding of what factors are. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. In simpler terms, if you divide a number by one of its factors, the result is another whole number.
Divisibility is the property of one number being divisible by another. This means the division results in a whole number quotient with no remainder. Understanding divisibility rules for certain numbers (like 2, 3, 5, etc.) can significantly speed up the process of finding factors.
Finding the Factors of 117: A Step-by-Step Approach
There are several ways to find the factors of 117. Let's explore a few methods:
Method 1: Systematic Listing
The most straightforward method is to systematically test numbers starting from 1. We'll check if each number divides 117 without leaving a remainder:
- 1: 117 divided by 1 is 117. Therefore, 1 and 117 are factors.
- 2: 117 is not divisible by 2 (it's an odd number).
- 3: The sum of the digits of 117 (1+1+7=9) is divisible by 3, so 117 is divisible by 3. 117 divided by 3 is 39. Therefore, 3 and 39 are factors.
- 4: 117 is not divisible by 4 (it's not divisible by 2 twice).
- 5: 117 is not divisible by 5 (it doesn't end in 0 or 5).
- 6: Since 117 is divisible by both 2 and 3, it's not divisible by 6.
- 7: 117 divided by 7 is approximately 16.7, so 7 is not a factor.
- 9: Since the sum of the digits is 9, 117 is divisible by 9. 117 divided by 9 is 13. Therefore, 9 and 13 are factors.
- 10: 117 is not divisible by 10.
- 11: 117 is not divisible by 11.
- 12: 117 is not divisible by 12.
- 13: We've already found 13 as a factor.
We continue this process until we reach the square root of 117 (approximately 10.8). After this point, we'll only find factor pairs we've already discovered.
Therefore, the factors of 117 are: 1, 3, 9, 13, 39, 117.
Method 2: Prime Factorization
Prime factorization is a more efficient method, especially for larger numbers. It involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself.
Let's find the prime factorization of 117:
- We know 117 is divisible by 3: 117 = 3 x 39
- 39 is also divisible by 3: 39 = 3 x 13
- 13 is a prime number.
Therefore, the prime factorization of 117 is 3 x 3 x 13, or 3² x 13.
Once we have the prime factorization, finding all the factors becomes easier. We can systematically combine the prime factors:
- 3¹ = 3
- 3² = 9
- 13¹ = 13
- 3¹ x 13¹ = 39
- 3² x 13¹ = 117
- 3⁰ x 13⁰ = 1
This method gives us the same factors as before: 1, 3, 9, 13, 39, 117.
Exploring Related Concepts: Divisibility Rules and Prime Numbers
Understanding divisibility rules helps in quickly identifying factors. Here are a few useful rules:
- Divisibility by 2: A number is divisible by 2 if it's even (ends in 0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 11: Subtract the sum of the digits in odd positions from the sum of the digits in even positions. If the result is divisible by 11, the original number is also divisible by 11.
Prime numbers form the building blocks of all other whole numbers. The prime factorization of a number is unique (apart from the order of the factors). This uniqueness is a fundamental concept in number theory. Understanding prime numbers is essential for various mathematical applications, including cryptography and computer science. The Sieve of Eratosthenes is a well-known algorithm for finding prime numbers within a given range.
Applications and Significance of Factorization
Finding factors isn't just an academic exercise. It has practical applications in various fields:
- Algebra: Factorization is crucial for simplifying algebraic expressions and solving equations.
- Number Theory: It's fundamental to understanding concepts like greatest common divisor (GCD) and least common multiple (LCM), which are vital in simplifying fractions and solving problems related to ratios and proportions.
- Cryptography: Prime factorization plays a critical role in modern cryptography, particularly in RSA encryption, a widely used algorithm for securing online communication.
- Computer Science: Algorithms for factorization are used in various computational tasks, including optimization problems and data analysis.
Conclusion: Beyond the Simple List of Factors
Determining the factors of 117, while seemingly straightforward, offers a gateway to understanding deeper mathematical principles. Moving beyond simply listing the factors—1, 3, 9, 13, 39, 117—to explore prime factorization and divisibility rules enhances our grasp of number theory and its applications. This understanding empowers us to approach more complex mathematical problems with confidence and efficiency, highlighting the importance of understanding the "why" behind the mathematical processes. The seemingly simple act of finding factors opens doors to a rich and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
How Do Humans And Other Consumers Obtain Nitrogen
Apr 08, 2025
-
1200 Square Feet To Square Meters
Apr 08, 2025
-
How To Find The Distance Between Two Parallel Lines
Apr 08, 2025
-
What Is 1 Out Of 3 In Percentage
Apr 08, 2025
-
Lcm Of 6 12 And 15
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 117 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.