Does A Circle Have Line Symmetry
Juapaving
Mar 30, 2025 · 5 min read
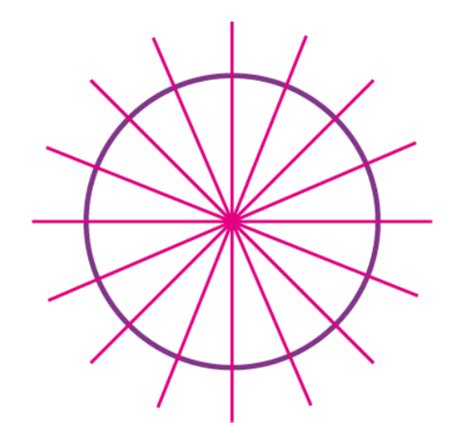
Table of Contents
Does a Circle Have Line Symmetry? A Comprehensive Exploration
The question of whether a circle possesses line symmetry might seem straightforward at first glance. However, a deeper dive reveals a fascinating interplay of geometry, transformations, and the very definition of symmetry itself. This article will explore the concept of line symmetry, analyze the properties of a circle, and ultimately provide a definitive answer, supported by clear explanations and illustrative examples.
Understanding Line Symmetry (Reflectional Symmetry)
Line symmetry, also known as reflectional symmetry, describes a geometric figure's property of being identical to its mirror image across a specific line. This line is called the line of symmetry or axis of symmetry. If you were to fold the figure along the line of symmetry, the two halves would perfectly overlap.
Think of a butterfly. Its wings are mirror images of each other; the line dividing the wings is its line of symmetry. Similarly, a square has four lines of symmetry: two diagonals and two lines connecting the midpoints of opposite sides.
Key characteristics of line symmetry:
- Reflection: The transformation involved is a reflection across the line of symmetry. Every point on one side of the line has a corresponding point on the other side, equidistant from the line.
- Congruence: The two halves created by the line of symmetry are congruent – identical in shape and size.
- Mapping: Each point on the figure maps to its mirror image across the line of symmetry.
Analyzing the Properties of a Circle
A circle is defined as a set of points in a plane that are equidistant from a given point called the center. This constant distance is known as the radius. Several key properties are relevant to our discussion of symmetry:
- Radial Symmetry: A circle exhibits radial symmetry, meaning it looks the same when rotated about its center by any angle. This is a different type of symmetry than line symmetry.
- Infinite Points: A circle contains an infinite number of points, all lying on its circumference.
- Constant Radius: The distance from the center to any point on the circumference is always the same (the radius).
- Uniformity: The circle's shape is consistent and uniform throughout its circumference.
Exploring Lines of Symmetry in a Circle
Now, let's directly address the question: Does a circle have line symmetry? The answer is yes, but with a crucial qualification.
A circle possesses an infinite number of lines of symmetry. Every line passing through the center of the circle acts as a line of symmetry. Let's break this down:
- Any Diameter is a Line of Symmetry: A diameter is a line segment that passes through the center of the circle and connects two points on the circumference. If you fold the circle along any diameter, the two halves will perfectly overlap. This demonstrates line symmetry.
- Infinite Diameters: Since you can draw an infinite number of diameters in a circle, each one serving as a line of symmetry, the circle has an infinite number of lines of symmetry.
Visualizing the Infinite Lines of Symmetry
Imagine drawing a line through the center of a circle. This line divides the circle into two perfectly congruent semicircles. Now, rotate this line slightly. You still have a line of symmetry. You can continue rotating it, creating an infinite number of lines, each acting as an axis of symmetry. This infinite number of lines of symmetry is a unique characteristic of the circle.
Distinguishing Line Symmetry from Radial Symmetry
It's crucial to differentiate between line symmetry and radial symmetry in the context of a circle. While a circle has both, they represent distinct geometric transformations:
- Line Symmetry (Reflection): Involves mirroring across a line.
- Radial Symmetry (Rotation): Involves rotating around a central point.
A circle has infinite lines of symmetry but only one center of radial symmetry. The presence of both these types of symmetry makes the circle a highly symmetrical shape.
Applications and Implications
The infinite line symmetry of a circle has implications across various fields:
- Engineering and Design: The circular shape is frequently used in engineering and design due to its inherent symmetry, strength, and efficiency in rotation.
- Mathematics: The concept of line symmetry in circles is fundamental to many mathematical concepts and theorems.
- Nature: Circles and near-circular shapes appear frequently in nature, often exhibiting line symmetry – think of the cross-section of a tree trunk or the ripples in a pond.
Beyond the Basic Circle: Variations and Extensions
The concept of line symmetry extends beyond the simple, perfect circle. Consider these variations:
- Incomplete Circles (Arcs): Arcs of circles may or may not have line symmetry depending on the specific arc and the placement of the line.
- Circles with Inscribed Shapes: A circle with inscribed shapes (like a square or triangle) will inherit some, but not necessarily all, of the circle's lines of symmetry.
- Circles with Added Features: A circle with additional features (lines, curves, etc.) added might lose some or all of its infinite lines of symmetry, depending on the nature of the additions.
Conclusion: The Circle's Profound Symmetry
The circle, in its elegant simplicity, possesses a remarkable property: an infinite number of lines of symmetry. This stems directly from its definition and the equidistant nature of its points from the center. Understanding this characteristic highlights the power and beauty of geometric symmetry and its importance in mathematics, science, engineering, and art. The seemingly simple question of whether a circle has line symmetry opens up a rich exploration of fundamental geometric concepts and their far-reaching applications. The infinite lines of symmetry of a circle not only define its unique visual characteristics but also contribute to its prevalence and usefulness across diverse disciplines.
Latest Posts
Latest Posts
-
A Rectangle Is A Square Always Sometimes Never
Apr 01, 2025
-
What Are The First 5 Multiples Of 2
Apr 01, 2025
-
What Is The Numeral For 42
Apr 01, 2025
-
Butter Melting Is A Physical Change
Apr 01, 2025
-
Lowest Common Multiple Of 20 And 8
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Does A Circle Have Line Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
