Does A Circle Have Any Lines Of Symmetry
Juapaving
Apr 01, 2025 · 5 min read
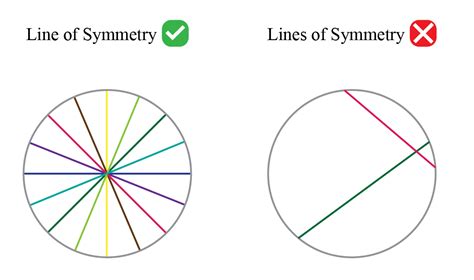
Table of Contents
- Does A Circle Have Any Lines Of Symmetry
- Table of Contents
- Does a Circle Have Any Lines of Symmetry? A Comprehensive Exploration
- Understanding Symmetry
- 1. Line Symmetry (Reflectional Symmetry)
- 2. Rotational Symmetry
- Analyzing Circular Symmetry: Lines of Symmetry
- Visualizing Infinite Lines of Symmetry
- Distinguishing Between Lines of Symmetry and Other Properties
- Applications of Circular Symmetry
- Beyond the Circle: Exploring Symmetry in Other Shapes
- Conclusion: The Enduring Significance of Circular Symmetry
- Latest Posts
- Latest Posts
- Related Post
Does a Circle Have Any Lines of Symmetry? A Comprehensive Exploration
The question of whether a circle possesses lines of symmetry might seem trivial at first glance. However, a deeper dive reveals fascinating insights into geometry, symmetry, and the very nature of mathematical definitions. This exploration will not only answer the question definitively but also delve into related concepts, exploring different types of symmetry and their applications.
Understanding Symmetry
Before tackling the specifics of circular symmetry, let's establish a firm understanding of what symmetry means in a geometric context. Symmetry, in its simplest form, refers to a balanced distribution of parts around a central point, line, or plane. In two-dimensional geometry, we primarily focus on two types of symmetry:
1. Line Symmetry (Reflectional Symmetry)
Line symmetry, also known as reflectional symmetry, exists when a figure can be folded along a line (called the axis of symmetry) such that the two halves perfectly overlap. Think of a butterfly; folding it along its central axis reveals perfect mirroring of its wings.
2. Rotational Symmetry
Rotational symmetry, on the other hand, occurs when a figure can be rotated about a central point (called the center of rotation) by a certain angle and still look exactly the same. A square, for instance, possesses rotational symmetry because it remains unchanged after rotations of 90°, 180°, and 270°.
Analyzing Circular Symmetry: Lines of Symmetry
Now, let's address the central question: does a circle possess any lines of symmetry? The answer is a resounding yes, and it's more profound than a simple affirmative. A circle exhibits an infinite number of lines of symmetry.
This seemingly extraordinary claim stems from the circle's fundamental definition: a set of points equidistant from a central point (the center). Consider any line passing through the center of the circle. This line acts as a perfect axis of symmetry. Folding the circle along such a line will result in a perfect overlap of the two halves.
Think of it this way:
- You can draw a diameter (a line segment passing through the center and connecting two opposite points on the circle) in any direction.
- Each diameter acts as a line of symmetry.
- Since you can draw an infinite number of diameters, a circle has an infinite number of lines of symmetry.
Visualizing Infinite Lines of Symmetry
Imagine drawing a diameter. Now, rotate that diameter by a tiny angle. You've created a new diameter, and hence, a new line of symmetry. You can continue this process infinitely, generating an infinite number of lines of symmetry. This illustrates the unparalleled symmetry of the circle.
Distinguishing Between Lines of Symmetry and Other Properties
It's crucial to differentiate between lines of symmetry and other properties that might seem related but are fundamentally distinct:
- Rotational Symmetry: While a circle possesses infinite lines of symmetry, it also exhibits rotational symmetry about its center. You can rotate a circle by any angle around its center, and it will remain unchanged. However, the infinite lines of symmetry are a distinct aspect of its overall symmetry.
- Centroid: The centroid of a circle, its geometric center, is the point around which it possesses rotational symmetry. It's not a line of symmetry itself, but it is crucial for understanding the circle's symmetrical nature.
- Diameter: While each diameter is a line of symmetry, it is not the only defining feature. The equidistance of all points from the center is the core definition that leads to the infinite lines of symmetry.
Applications of Circular Symmetry
The remarkable symmetry of a circle is not just a mathematical curiosity; it finds significant applications in numerous fields:
- Engineering and Design: Circular structures are prevalent due to their inherent strength and stability. The symmetrical distribution of stress allows for efficient load-bearing. Wheels, gears, and many rotational components in machines leverage the circular symmetry.
- Physics: Circular motion and rotation are fundamental concepts in physics. The symmetry of a circle simplifies calculations involving orbital motion, planetary systems, and the behavior of rotating objects.
- Art and Architecture: Circles and spheres, embodying perfect symmetry, have been used in art and architecture for millennia to convey notions of harmony, balance, and perfection. Think of the iconic Pantheon in Rome or countless mandala designs.
- Nature: Circular forms frequently appear in nature, from the rings of a tree trunk to the orbits of celestial bodies. These natural circular shapes often reflect underlying principles of symmetry and efficiency.
Beyond the Circle: Exploring Symmetry in Other Shapes
Understanding circular symmetry provides a solid foundation for exploring symmetry in other shapes. While a circle has infinite lines of symmetry, other shapes have varying numbers, or none at all. Consider these examples:
- Square: A square has four lines of symmetry: two diagonals and two lines connecting the midpoints of opposite sides. It also has rotational symmetry.
- Equilateral Triangle: An equilateral triangle has three lines of symmetry, each connecting a vertex to the midpoint of the opposite side.
- Rectangle (non-square): A rectangle has two lines of symmetry, each connecting the midpoints of opposite sides.
- Irregular Shapes: Many shapes have no lines of symmetry, showcasing the varied nature of symmetry in geometry.
Conclusion: The Enduring Significance of Circular Symmetry
The question of whether a circle has lines of symmetry leads us on a fascinating journey into the realm of geometry and symmetry. The answer—an infinite number of lines of symmetry—highlights the unique and profound symmetrical properties of the circle. This inherent symmetry extends far beyond theoretical mathematics, impacting engineering, physics, art, and nature. Understanding circular symmetry, therefore, provides not only a deeper appreciation of mathematical concepts but also a broader perspective on the elegant principles that govern the world around us. It’s a testament to the power of mathematical definitions to reveal underlying beauty and order in the universe. The seemingly simple circle, with its infinite lines of symmetry, remains a rich source of wonder and exploration for mathematicians and enthusiasts alike.
Latest Posts
Latest Posts
-
Fluid Part Of Blood After Removal Of Corpuscles Is
Apr 05, 2025
-
Is A Substance In Which Another Substance Is Dissolved
Apr 05, 2025
-
Empirical Formula Calculator For Ionic Compounds
Apr 05, 2025
-
How Much Do Your Bones Weigh
Apr 05, 2025
-
Correctly Label The Following Anatomical Parts Of A Kidney
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Does A Circle Have Any Lines Of Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
