Displacement Is How Far An Object Moves
Juapaving
Apr 02, 2025 · 6 min read
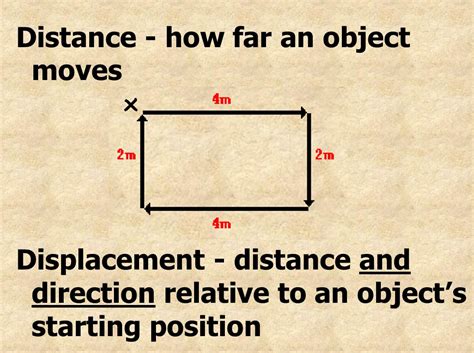
Table of Contents
Displacement: How Far an Object Moves – A Comprehensive Guide
Understanding displacement is fundamental to grasping the concepts of motion and mechanics. While it might seem simple at first glance – "how far an object moves" – a deeper dive reveals nuances that distinguish it from distance and are crucial in various scientific and engineering applications. This comprehensive guide will explore displacement in detail, covering its definition, calculation, vector nature, applications, and its relationship to other key concepts like velocity and acceleration.
Defining Displacement: More Than Just Distance
Displacement, in the simplest terms, is the change in position of an object. It's a vector quantity, meaning it possesses both magnitude (how far the object moved) and direction. This is where it significantly differs from distance, which is a scalar quantity and only considers the total ground covered. Consider walking 10 meters east, then 5 meters west. Your distance traveled is 15 meters (10 + 5). However, your displacement is only 5 meters east (10 - 5). The final position relative to the starting point is what determines displacement.
Key Differences Between Distance and Displacement:
- Scalar vs. Vector: Distance is a scalar (magnitude only), while displacement is a vector (magnitude and direction).
- Path Dependence vs. Path Independence: Distance depends on the path taken; displacement only considers the initial and final positions.
- Units: Both are typically measured in meters (m), kilometers (km), or other units of length.
Calculating Displacement: A Vector Approach
Calculating displacement involves determining the vector that connects the object's initial and final positions. This often involves using coordinate systems (like Cartesian coordinates) to represent these positions.
1. Using Cartesian Coordinates:
Let's say an object moves from point A (x₁, y₁) to point B (x₂, y₂). The displacement vector, denoted as Δr (delta r), can be calculated as:
Δr = (x₂ - x₁)î + (y₂ - y₁)ĵ
where î and ĵ are unit vectors in the x and y directions, respectively. The magnitude of the displacement (the distance between A and B) is given by the Pythagorean theorem:
|Δr| = √((x₂ - x₁)² + (y₂ - y₁)²)
2. Displacement in Multiple Dimensions:
The concept extends readily to three dimensions (and even higher dimensions in more advanced physics). In 3D space, with points A(x₁, y₁, z₁) and B(x₂, y₂, z₂), the displacement vector is:
Δr = (x₂ - x₁)î + (y₂ - y₁)ĵ + (z₂ - z₁)k̂
where k̂ is the unit vector in the z-direction. The magnitude is calculated using a 3D version of the Pythagorean theorem.
3. Graphical Representation:
Displacement can be effectively represented graphically using arrows. The arrow's length corresponds to the magnitude of the displacement, and its direction indicates the direction of displacement. This is particularly useful for visualizing displacement in scenarios involving multiple movements.
Displacement in Real-World Applications
The concept of displacement is not just a theoretical construct; it finds practical application in numerous fields:
1. Navigation and GPS:
GPS systems rely heavily on displacement calculations to determine the position and distance between locations. The system continuously tracks changes in position to provide accurate navigation. It calculates displacement vectors constantly to update your location and provide directions.
2. Robotics and Automation:
In robotics, precise control of robot movements necessitates accurate displacement calculations. Robots need to know their exact position and orientation to perform tasks correctly. Displacement vectors are used to program movements, ensuring robots move precisely to specified points.
3. Physics and Engineering:
Displacement is a fundamental concept in classical mechanics, used in analyzing projectile motion, oscillatory motion (like pendulums), and the motion of objects under various forces. In engineering, it's crucial in designing structures, calculating stresses and strains, and analyzing the movement of components in machinery.
4. Meteorology and Oceanography:
In meteorology, tracking the movement of weather systems involves calculating the displacement of air masses. Similarly, in oceanography, tracking ocean currents relies on understanding the displacement of water masses over time.
5. Sports Analytics:
Sports analytics utilizes displacement data to analyze player movements, optimize strategies, and evaluate player performance. Tracking the displacement of athletes on the field or court provides insights into their speed, agility, and efficiency.
Displacement and its Relationship to Velocity and Acceleration
Displacement is intrinsically linked to velocity and acceleration. These concepts build upon each other to provide a comprehensive description of an object's motion.
1. Velocity: The Rate of Change of Displacement
Velocity is a vector quantity representing the rate of change of displacement with respect to time. It describes both the speed and direction of an object's movement. Average velocity is calculated as:
Average Velocity (v) = Δr / Δt
where Δt is the change in time. Instantaneous velocity considers the rate of change at a specific instant.
2. Acceleration: The Rate of Change of Velocity
Acceleration, also a vector quantity, represents the rate of change of velocity with respect to time. It describes how quickly the velocity of an object is changing. Average acceleration is calculated as:
Average Acceleration (a) = Δv / Δt
where Δv is the change in velocity.
3. Connecting Displacement, Velocity, and Acceleration:
These three quantities are interconnected through calculus. Velocity is the derivative of displacement with respect to time, and acceleration is the derivative of velocity (or the second derivative of displacement) with respect to time. Understanding these relationships is critical for solving problems involving motion.
Advanced Concepts and Considerations
While the basic concept of displacement is relatively straightforward, some more advanced considerations add complexity and refine our understanding:
1. Non-uniform Motion:
The calculations presented earlier assume constant velocity or acceleration. In many real-world scenarios, motion is non-uniform – velocity and acceleration change over time. In these cases, calculus (integration and differentiation) is necessary for accurate displacement calculations.
2. Curvilinear Motion:
Motion along a curved path presents challenges for calculating displacement. While the basic principle remains – change in position – determining the displacement vector requires vector calculus techniques.
3. Relative Displacement:
The concept of displacement can be relative to a specific frame of reference. For instance, an object's displacement within a moving vehicle is different from its displacement relative to the ground. Considering the frame of reference is crucial for accurate analysis.
4. Displacement in Rotating Systems:
In rotating systems, displacement becomes more complex, requiring the consideration of angular displacement and rotational velocity. This area falls under the domain of rotational kinematics.
Conclusion: Understanding Displacement's Importance
Displacement, although seemingly simple – "how far an object moves" – is a fundamental concept in physics and engineering with far-reaching applications. Its vector nature distinguishes it from distance, emphasizing both magnitude and direction. Understanding its relationship with velocity and acceleration, coupled with the ability to calculate displacement in various scenarios, is crucial for accurately describing and analyzing motion in diverse fields. Whether navigating with GPS, designing robotic systems, or analyzing athletic performance, the concept of displacement serves as a cornerstone for a comprehensive understanding of motion. Mastering this concept opens the door to a deeper understanding of more complex dynamics and kinematic principles.
Latest Posts
Latest Posts
-
Whats The Square Root Of 30
Apr 03, 2025
-
How Many Feet Is 18 Yards
Apr 03, 2025
-
Facts And Statistics Collected Together For Reference Or Analysis
Apr 03, 2025
-
118 Inches Is How Many Feet
Apr 03, 2025
-
What Is The Highest Common Factor Of 16 And 24
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Displacement Is How Far An Object Moves . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
