What's The Square Root Of 30
Juapaving
Apr 03, 2025 · 5 min read
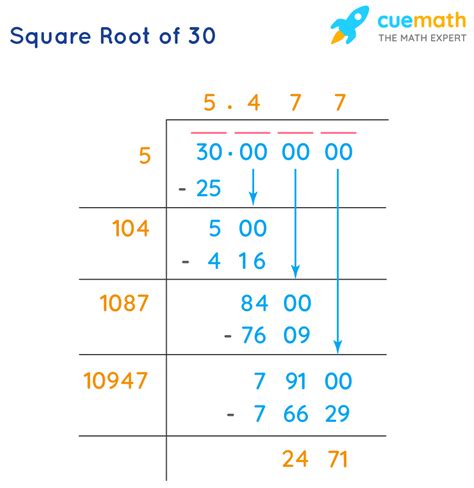
Table of Contents
What's the Square Root of 30? A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What's the square root of 30?", opens a door to a fascinating exploration of mathematics, specifically the realm of irrational numbers and the various methods used to approximate their values. While a precise, finite decimal representation doesn't exist, we can delve into several approaches to understand and calculate a close approximation of √30.
Understanding Irrational Numbers
Before we embark on the journey of approximating √30, let's establish a foundational understanding of irrational numbers. An irrational number is a real number that cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating. Famous examples include π (pi) and e (Euler's number). The square root of any non-perfect square (a number that isn't the product of an integer multiplied by itself) is also irrational. Since 30 is not a perfect square (no integer multiplied by itself equals 30), √30 is an irrational number.
Why is √30 Irrational?
This stems from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Let's assume, for the sake of contradiction, that √30 is rational. This means we could express it as a fraction a/b, where 'a' and 'b' are integers, and b is not zero, and the fraction is in its simplest form (a and b share no common factors).
Then, we have (a/b)² = 30. This simplifies to a² = 30b². From this equation, we can deduce that a² must be divisible by 30. Since 30 = 2 × 3 × 5, this implies that 'a' must be divisible by 2, 3, and 5. Therefore, we can rewrite 'a' as 2 × 3 × 5 × k = 30k, where 'k' is another integer.
Substituting this back into the equation, we get (30k)² = 30b², which simplifies to 900k² = 30b². Dividing both sides by 30, we get 30k² = b². This shows that b² is also divisible by 30, and therefore 'b' must also be divisible by 2, 3, and 5.
This contradicts our initial assumption that a/b is in its simplest form, as both 'a' and 'b' are divisible by 2, 3, and 5. This contradiction proves that our initial assumption—that √30 is rational—must be false. Therefore, √30 is indeed irrational.
Methods for Approximating √30
Since we can't express √30 exactly, we need approximation methods. Several techniques provide increasingly accurate estimations.
1. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to get closer to the actual square root. The formula is:
x_(n+1) = (x_n + S/x_n) / 2
Where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- S is the number whose square root we're seeking (in our case, 30)
Let's start with an initial guess of x_0 = 5 (because 5² = 25, which is close to 30).
- Iteration 1: x_1 = (5 + 30/5) / 2 = 5.5
- Iteration 2: x_2 = (5.5 + 30/5.5) / 2 ≈ 5.477
- Iteration 3: x_3 = (5.477 + 30/5.477) / 2 ≈ 5.477225575
As you can see, the method rapidly converges towards a more accurate approximation. Each iteration refines the estimate further. Continuing this process will yield increasingly precise results.
2. Using a Calculator or Computer
Modern calculators and computer software are equipped to calculate square roots to a high degree of accuracy. Simply inputting √30 will return a value like 5.477225575... This is a computationally efficient method, but it doesn't offer the same mathematical insight as other techniques.
3. Linear Approximation
This involves finding a tangent line to the function f(x) = √x at a point close to 30. Let's use the point x = 25 (since √25 = 5 is easily calculable). The derivative of f(x) = √x is f'(x) = 1/(2√x). At x = 25, the derivative is 1/(2√25) = 1/10 = 0.1.
The equation of the tangent line is:
y - 5 = 0.1(x - 25)
Plugging in x = 30, we get:
y = 5 + 0.1(30 - 25) = 5 + 0.5 = 5.5
This method gives a less precise approximation than the Babylonian method, but it demonstrates the use of calculus for approximation.
4. Numerical Methods (Newton-Raphson)
The Newton-Raphson method is another powerful iterative technique for finding roots of equations. It's particularly useful for finding square roots. The formula is:
x_(n+1) = x_n - f(x_n)/f'(x_n)
Where f(x) = x² - 30 (we're finding the root of this equation, which is √30) and f'(x) = 2x. Again, starting with an initial guess of 5:
- Iteration 1: x_1 = 5 - (5² - 30) / (2 * 5) = 5.5
- Iteration 2: x_2 = 5.5 - (5.5² - 30) / (2 * 5.5) ≈ 5.4773
This method converges quickly to a very accurate approximation, similar to the Babylonian method.
Applications of √30
Understanding and approximating the square root of 30, while seemingly abstract, has practical applications in various fields:
- Geometry: Calculating the diagonal of a rectangle with sides of length 5 and √5. Pythagorean theorem plays a pivotal role here.
- Physics: Many physical phenomena involve square roots, such as calculations related to velocity, acceleration, and energy.
- Engineering: Designing structures and calculating forces often requires precise calculations that may involve irrational numbers like √30.
- Computer Graphics: Creating realistic simulations and animations necessitate high-precision calculations, including approximating square roots.
- Financial Modeling: Certain financial calculations involve square roots for scenarios like portfolio optimization and risk management.
Conclusion: The Ongoing Pursuit of Precision
While we cannot express √30 as a finite decimal, the various approximation methods discussed provide accurate estimations for practical purposes. The Babylonian method, Newton-Raphson method, and even the simpler linear approximation offer different approaches to understanding and calculating this irrational number. The choice of method depends on the desired level of accuracy and the available computational resources. The quest to understand irrational numbers like √30 highlights the beauty and complexity of mathematics and its pervasive role in our world. The journey from a simple question to understanding the intricacies of approximation techniques underscores the power of mathematical exploration and its continuous relevance across diverse disciplines.
Latest Posts
Latest Posts
-
How Tall Is 90 Inches In Feet
Apr 04, 2025
-
Difference Between Independent Assortment And Segregation
Apr 04, 2025
-
Difference Between Spongy And Compact Bone
Apr 04, 2025
-
D How Is The Energy Produced By Respiration Stored
Apr 04, 2025
-
The Functional And Structural Unit Of The Kidneys Is The
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
