Difference Between Distance And Displacement For Class 9
Juapaving
Mar 27, 2025 · 6 min read
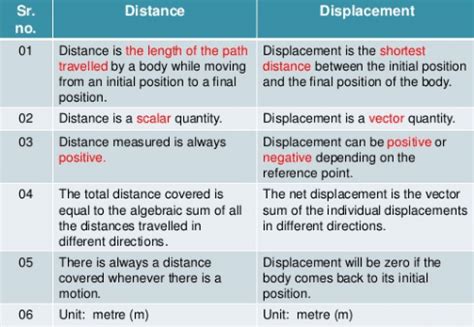
Table of Contents
Unveiling the Mystery: Distance vs. Displacement for Class 9
Understanding the difference between distance and displacement is crucial for grasping fundamental concepts in physics, particularly in the study of motion. While seemingly similar, these two terms represent distinct physical quantities with different characteristics and applications. This comprehensive guide delves into the nuances of distance and displacement, providing clear explanations, illustrative examples, and practical applications relevant to a Class 9 understanding.
What is Distance?
Distance is a scalar quantity that refers to the total length of the path traveled by an object. It's simply how much ground an object has covered during its movement, regardless of the direction. Think of it as the odometer reading in your car – it keeps accumulating the total kilometers driven, irrespective of the route taken.
Key Characteristics of Distance:
- Scalar: It only has magnitude (size or value), not direction. You might travel 10 kilometers, but that doesn't tell you where you ended up.
- Always positive: Distance can never be negative because it's a measure of length.
- Dependent on the path: The distance traveled will change if the path taken changes, even if the starting and ending points remain the same.
Example: Imagine you walk 5 meters east, then 3 meters north, and finally 2 meters west. The total distance you've traveled is 5 + 3 + 2 = 10 meters.
Understanding Scalar Quantities
A scalar quantity is completely described by its magnitude (size or numerical value) alone. It does not involve direction. Other examples of scalar quantities include:
- Speed: How fast an object is moving.
- Mass: The amount of matter in an object.
- Temperature: A measure of hotness or coldness.
- Time: The duration of an event.
- Energy: The capacity to do work.
What is Displacement?
Displacement, unlike distance, is a vector quantity. This means it possesses both magnitude (size) and direction. Displacement refers to the shortest distance between the starting point and the ending point of an object's motion. It's a straight line connecting the initial and final positions, irrespective of the actual path followed.
Key Characteristics of Displacement:
- Vector: It has both magnitude and direction (e.g., 10 meters east).
- Can be positive, negative, or zero: The sign indicates direction. Positive might represent movement in one direction (e.g., east), while negative represents the opposite direction (e.g., west). Zero displacement occurs when the starting and ending points are the same.
- Independent of the path: The displacement only depends on the initial and final positions, not the route followed.
Example: Using the same scenario from the distance example (5 meters east, 3 meters north, 2 meters west), the displacement can be calculated using vector addition. The net eastward movement is 5 meters - 2 meters = 3 meters east. The northward movement is 3 meters. The overall displacement is the hypotenuse of a right-angled triangle with sides of 3 meters and 3 meters. Using the Pythagorean theorem (a² + b² = c²), the magnitude of the displacement is √(3² + 3²) ≈ 4.24 meters. The direction would be approximately northeast.
Understanding Vector Quantities
A vector quantity requires both magnitude and direction for complete description. Other examples include:
- Velocity: The rate of change of displacement.
- Acceleration: The rate of change of velocity.
- Force: A push or pull that can cause acceleration.
- Momentum: The product of mass and velocity.
Distance vs. Displacement: A Comparative Table
| Feature | Distance | Displacement |
|---|---|---|
| Type | Scalar | Vector |
| Magnitude | Always positive | Can be positive, negative, or zero |
| Direction | No direction | Has direction |
| Path Dependence | Dependent on the path taken | Independent of the path taken |
| Measurement | Total length of the path traveled | Shortest distance between start and end |
Illustrative Examples to Solidify Understanding
Let's delve into more complex examples to further clarify the difference:
Example 1: Circular Motion
Imagine a runner completing one lap around a 400-meter circular track.
- Distance: The distance covered is 400 meters.
- Displacement: The displacement is 0 meters because the runner ends up at the same starting point.
Example 2: A More Complex Path
Consider a car traveling 5 km north, then 3 km east, and finally 2 km south.
- Distance: The total distance is 5 km + 3 km + 2 km = 10 km.
- Displacement: To find the displacement, we can use vector addition. The net northward movement is 5 km - 2 km = 3 km north. The eastward movement is 3 km east. The magnitude of the displacement is √(3² + 3²) ≈ 4.24 km. The direction is approximately northeast.
Example 3: Back and Forth Motion
A ball rolls 5 meters to the right, then 3 meters to the left.
- Distance: The total distance is 5 m + 3 m = 8 m.
- Displacement: The displacement is 5 m - 3 m = 2 m to the right.
Real-world Applications
The concepts of distance and displacement are fundamental to numerous real-world applications:
- Navigation: GPS systems use displacement calculations to determine the shortest route between two locations.
- Mapping: Cartography relies on distance and displacement measurements to represent geographical features accurately.
- Sports: Analyzing an athlete's movement, such as in running or swimming, often involves calculating both distance and displacement to assess performance.
- Robotics: Programming robots to navigate requires precise understanding and calculation of distance and displacement.
- Physics: Many physics problems, particularly those dealing with kinematics (the study of motion), require distinguishing between distance and displacement for accurate calculations.
Solving Problems Involving Distance and Displacement
Let's tackle some problems that will reinforce your understanding:
Problem 1: A bird flies 20 meters east, then 15 meters north, and finally 10 meters west. Calculate the total distance and displacement.
Solution:
- Distance: 20 m + 15 m + 10 m = 45 m
- Displacement: Net eastward movement: 20 m - 10 m = 10 m east. Northward movement: 15 m north. Magnitude of displacement: √(10² + 15²) ≈ 18 m. Direction: Approximately northeast.
Problem 2: A car travels around a square track with sides of 100 meters. Calculate the distance and displacement after one complete lap.
Solution:
- Distance: 100 m × 4 = 400 m
- Displacement: 0 m (The car ends up at the starting point).
Problem 3: A person walks 5 km due north, then 12 km due east. What is the distance and displacement?
Solution:
- Distance: 5 km + 12 km = 17 km
- Displacement: Using the Pythagorean theorem: √(5² + 12²) = 13 km. The direction is northeast (you can specify the exact angle using trigonometry).
Conclusion
The distinction between distance and displacement is fundamental in understanding motion. While distance measures the total path length, displacement focuses on the straight-line distance between the starting and ending points, incorporating direction. Mastering the difference between these two concepts is essential for success in physics and many other scientific fields. By understanding their unique characteristics and applications, you can confidently tackle more complex problems related to motion and navigation. Remember to always consider both magnitude and direction when dealing with vector quantities like displacement. Practice solving various problems to further solidify your understanding.
Latest Posts
Latest Posts
-
What Is A Factor Of 63
Mar 30, 2025
-
An Amoeba Engulfs A Particle Of Food
Mar 30, 2025
-
Type Of Joint Between Axis And Atlas
Mar 30, 2025
-
5 Letter Words End With Eat
Mar 30, 2025
-
A Letter That Represents A Number
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Difference Between Distance And Displacement For Class 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
