Determine The Total Number Of Roots Of Each Polynomial Function.
Juapaving
Apr 03, 2025 · 5 min read
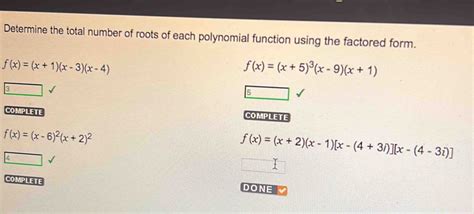
Table of Contents
Determining the Total Number of Roots of Polynomial Functions
Understanding the total number of roots a polynomial function possesses is fundamental in algebra and numerous applications across various fields like engineering, physics, and computer science. This comprehensive guide will delve into the intricacies of determining the total number of roots for polynomial functions, exploring different theorems and techniques to solve these problems effectively. We'll move from basic concepts to more advanced strategies, ensuring a solid grasp of this crucial mathematical principle.
The Fundamental Theorem of Algebra: The Cornerstone
The cornerstone of understanding the number of roots of a polynomial function is the Fundamental Theorem of Algebra. This theorem states that every non-constant polynomial with complex coefficients has at least one complex root. A crucial implication of this theorem is that a polynomial of degree n (where n is a positive integer) has exactly n complex roots, counting multiplicity.
What does "counting multiplicity" mean? This means that a root can appear more than once. For example, the polynomial x² - 2x + 1 = (x-1)(x-1) = (x-1)² has a root of x = 1 with multiplicity 2. It has two roots, but they are both the same value.
Example:
Consider the polynomial function f(x) = x³ - 6x² + 11x - 6. This is a polynomial of degree 3. Therefore, according to the Fundamental Theorem of Algebra, it has exactly three complex roots.
Finding the Roots: Techniques and Methods
While the Fundamental Theorem of Algebra tells us how many roots exist, it doesn't directly tell us what those roots are. Finding the actual roots can be challenging and often requires a combination of techniques:
1. Factoring: The Simplest Approach
Factoring is the most straightforward method for finding the roots of a polynomial. If you can factor the polynomial into linear factors (factors of the form (x - r), where 'r' is a root), then the roots are readily apparent.
Example:
f(x) = x² - 5x + 6 can be factored as (x - 2)(x - 3). Therefore, the roots are x = 2 and x = 3.
2. Quadratic Formula: Solving Second-Degree Polynomials
For quadratic polynomials (polynomials of degree 2), the quadratic formula provides a direct method for finding the roots:
For a quadratic equation of the form ax² + bx + c = 0, the roots are given by:
x = (-b ± √(b² - 4ac)) / 2a
The term b² - 4ac is called the discriminant. The discriminant provides information about the nature of the roots:
- b² - 4ac > 0: Two distinct real roots.
- b² - 4ac = 0: One real root (with multiplicity 2).
- b² - 4ac < 0: Two distinct complex roots (conjugate pairs).
3. Rational Root Theorem: Narrowing Down Possibilities
The Rational Root Theorem helps narrow down the possible rational roots (roots that are fractions) of a polynomial with integer coefficients. It states that if a polynomial has a rational root p/q (where p and q are integers and q ≠ 0), then p must be a factor of the constant term and q must be a factor of the leading coefficient.
Example:
For the polynomial f(x) = 2x³ - 5x² + x + 2, the possible rational roots are ±1, ±2, ±1/2. You can then test these values to see if they are actual roots.
4. Numerical Methods: Approximating Roots
For higher-degree polynomials or polynomials that are difficult to factor, numerical methods are often necessary to approximate the roots. These methods include:
- Newton-Raphson method: An iterative method that refines an initial guess to find a root.
- Bisection method: A method that repeatedly divides an interval containing a root in half.
5. Graphical Methods: Visualizing Roots
Graphing the polynomial function can provide a visual representation of the real roots. The x-intercepts of the graph correspond to the real roots of the polynomial. While this method doesn't directly give the exact values of the roots, it's helpful in visualizing the number and approximate location of the real roots.
Complex Roots and Conjugate Pairs
The Fundamental Theorem of Algebra guarantees that a polynomial of degree n has n complex roots. However, complex roots always appear in conjugate pairs. This means that if a + bi is a root (where a and b are real numbers and i is the imaginary unit), then a - bi is also a root.
Polynomials with Real Coefficients: A Special Case
When dealing with polynomials that have only real coefficients, the following observations are crucial:
- The non-real roots (complex roots) always come in conjugate pairs.
- If the degree of the polynomial is odd, there must be at least one real root. This is because complex roots come in pairs, and an odd number cannot be composed entirely of pairs.
Applications of Finding Roots
The ability to determine the number and values of roots of polynomial functions is critical across various disciplines:
- Engineering: Designing structures, analyzing systems' stability, and modeling physical phenomena.
- Physics: Solving equations of motion, describing wave behavior, and analyzing oscillations.
- Computer Science: Developing algorithms, solving optimization problems, and creating computer graphics.
- Economics and Finance: Modeling economic growth, analyzing investment strategies, and pricing derivatives.
Advanced Concepts and Extensions
The discussion above covers the fundamental principles. More advanced topics include:
- Multiplicity of Roots: Understanding how repeated roots affect the behavior of the polynomial function (e.g., tangent points on a graph).
- Descartes' Rule of Signs: A method for determining the maximum number of positive and negative real roots.
- Sturm's Theorem: A more sophisticated technique for determining the number of real roots within a given interval.
Conclusion
Determining the total number of roots of a polynomial function is a cornerstone of algebra with wide-ranging applications. By understanding the Fundamental Theorem of Algebra and employing appropriate techniques like factoring, the quadratic formula, the Rational Root Theorem, and numerical methods, we can effectively find the roots and analyze the behavior of polynomial functions. Remember to consider the multiplicity of roots and the nature of complex roots (conjugate pairs) for a complete understanding. Mastering these concepts provides a solid foundation for tackling more complex mathematical problems and opens doors to numerous applications in various fields. The exploration of advanced methods like Descartes' Rule of Signs and Sturm's Theorem offers further refinement and deeper insights into the intricacies of polynomial roots.
Latest Posts
Latest Posts
-
Who Is Credited For Discovering Cells
Apr 03, 2025
-
Is 7 A Prime Or Composite Number
Apr 03, 2025
-
Are Humans Warm Blooded Or Cold Blooded
Apr 03, 2025
-
What Is 0 08 As A Percent
Apr 03, 2025
-
How Many Chambers Does A Fish Heart Have
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Determine The Total Number Of Roots Of Each Polynomial Function. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
