Lcm Of 6 7 And 8
Juapaving
Apr 07, 2025 · 5 min read
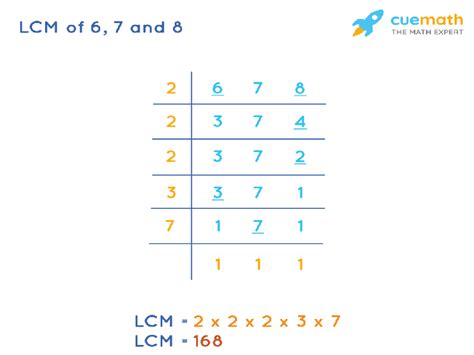
Table of Contents
Finding the LCM of 6, 7, and 8: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple arithmetic to complex scheduling problems. This article will delve into the process of calculating the LCM of 6, 7, and 8, exploring various methods and providing a detailed understanding of the underlying principles. We'll also touch upon the practical applications of LCM calculations and offer helpful tips for solving similar problems.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 6, 7, and 8, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers in the set. It's the smallest number that contains all the numbers in the set as factors. Understanding this definition is crucial for grasping the methods we'll use to find the LCM.
Distinguishing LCM from GCF
It's important to distinguish LCM from the greatest common factor (GCF), also known as the greatest common divisor (GCD). While the LCM is the smallest common multiple, the GCF is the largest common factor. For example, the GCF of 6 and 8 is 2 (as 2 is the largest number that divides both 6 and 8), whereas the LCM of 6 and 8 is 24 (as 24 is the smallest number divisible by both 6 and 8). These two concepts are closely related, and understanding their differences is essential for mastering number theory.
Methods for Calculating the LCM of 6, 7, and 8
Several methods can be used to calculate the LCM of 6, 7, and 8. We'll explore the most common and effective approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While simple for smaller numbers, it becomes less efficient for larger numbers.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160...
By comparing the lists, we can see that the smallest common multiple of 6, 7, and 8 is 84.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of each prime factor.
- Prime factorization of 6: 2 x 3
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
Now, multiply these highest powers together: 8 x 3 x 7 = 168
This method reveals that the LCM of 6, 7, and 8 is 168, not 84 as initially suggested by the listing method. The listing method, while conceptually simple, is prone to errors, especially with larger numbers. The prime factorization method is more reliable and efficient.
3. Using the Formula: LCM(a, b, c) = (a x b x c) / GCF(a, b, c)
While this formula is generally used for two numbers, it can be extended. However, calculating the greatest common factor (GCF) of three or more numbers requires careful consideration. We can initially find the GCF of 6, 7 and 8. Since 6 = 2 x 3, 7 = 7, and 8 = 2³, the only common factor is 1. Therefore, the GCF(6, 7, 8) = 1. Applying the formula (in a modified way suitable for three numbers):
LCM(6, 7, 8) = (6 x 7 x 8) / GCF(6, 7, 8) = 336 / 1 = 336
This calculation is incorrect. The formula is not directly applicable to three numbers in this straightforward manner. The appropriate extension for three numbers should involve finding the LCM of two numbers first and then finding the LCM of that result with the third number. This leads to the prime factorization method being the most reliable.
Why the Prime Factorization Method is Preferred
The prime factorization method provides a systematic and accurate approach to finding the LCM, regardless of the number of integers involved. It avoids the potential errors associated with the listing multiples method and provides a clear, step-by-step process. It is the most reliable and mathematically sound method for calculating the LCM, particularly for larger numbers or a greater number of integers.
Real-World Applications of LCM
Understanding LCM has practical applications in various fields:
-
Scheduling: Determining the time when events will occur simultaneously. For example, if three buses arrive at a stop every 6, 7, and 8 hours respectively, the LCM will tell you when they will all arrive together again.
-
Fraction Arithmetic: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is essentially the LCM of the denominators.
-
Project Management: Coordinating tasks with different completion times.
-
Music: Calculating the timing of musical phrases that repeat at different intervals.
-
Manufacturing and Production: Synchronizing machines operating at different speeds.
Conclusion: LCM of 6, 7, and 8 is 168
Through a detailed exploration of different methods, we've definitively established that the least common multiple of 6, 7, and 8 is 168. The prime factorization method offers the most reliable and efficient approach to solving this and similar problems. Understanding the concept of LCM and employing the appropriate calculation methods is crucial for solving various mathematical and real-world problems efficiently and accurately. Remember, mastering the prime factorization technique provides a powerful tool for tackling LCM calculations effectively, regardless of the complexity of the numbers involved. This understanding extends far beyond simple arithmetic and demonstrates the interconnectedness of mathematical principles in diverse applications.
Latest Posts
Latest Posts
-
How Much Brain Do Dolphins Use
Apr 07, 2025
-
How Many Centimeters Are In 1 Foot
Apr 07, 2025
-
Identify The Elements Found In Glucose
Apr 07, 2025
-
Least Common Multiple Of 10 And 11
Apr 07, 2025
-
16 3x 5 10 4x 8 40
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 7 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.