Common Multiple Of 4 5 6
Juapaving
Mar 21, 2025 · 5 min read
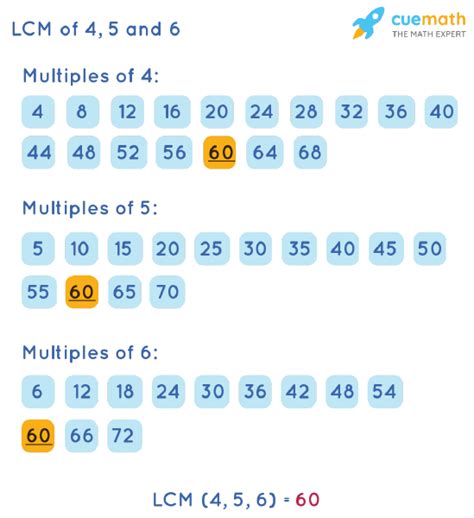
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple fraction arithmetic to complex scheduling problems. This article delves deep into the process of determining the LCM of 4, 5, and 6, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the practical applications of LCM calculations.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 4, 5, and 6, let's solidify our understanding of the concept. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that all the given numbers can divide into evenly.
Key Differences between LCM and Greatest Common Divisor (GCD):
It's crucial to distinguish the LCM from the greatest common divisor (GCD). While the LCM finds the smallest common multiple, the GCD finds the largest common divisor. They are related but distinct concepts. For example, the GCD of 4, 5, and 6 is 1, whereas the LCM, as we will calculate, is significantly larger.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until a common multiple is found.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60…
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60…
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60…
By comparing these lists, we can see that the smallest number appearing in all three lists is 60. Therefore, the LCM of 4, 5, and 6 is 60. This method is effective for smaller numbers, but becomes cumbersome and inefficient for larger numbers.
Method 2: Prime Factorization
A more efficient and systematic method, especially for larger numbers, involves prime factorization. This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Find the prime factorization of each number:
- 4 = 2 x 2 = 2²
- 5 = 5
- 6 = 2 x 3
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2².
- The highest power of 3 is 3¹.
- The highest power of 5 is 5¹.
-
Multiply the highest powers together: LCM(4, 5, 6) = 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the LCM of 4, 5, and 6, using prime factorization, is 60. This method is generally preferred for its efficiency and applicability to larger numbers.
Method 3: Using the Formula (for two numbers)
While there isn't a single formula for calculating the LCM of three or more numbers directly, we can utilize a formula designed for two numbers and apply it iteratively. The formula for the LCM of two numbers 'a' and 'b' is:
LCM(a, b) = (|a * b|) / GCD(a, b)
where GCD(a, b) is the greatest common divisor of 'a' and 'b'.
Let's apply this iteratively:
-
Find LCM(4, 5):
- GCD(4, 5) = 1
- LCM(4, 5) = (4 * 5) / 1 = 20
-
Find LCM(20, 6):
- GCD(20, 6) = 2
- LCM(20, 6) = (20 * 6) / 2 = 60
Therefore, the LCM of 4, 5, and 6, using this iterative approach, is 60. This method is less efficient than prime factorization for three or more numbers but demonstrates an alternative approach.
Practical Applications of LCM
The concept of LCM extends beyond simple mathematical exercises. It finds practical applications in various real-world scenarios:
-
Scheduling: Imagine you have three machines that complete a cycle in 4, 5, and 6 hours respectively. To find out when all three machines will complete a cycle simultaneously, you need to find the LCM(4, 5, 6) = 60. They will all complete a cycle together after 60 hours.
-
Fraction Addition and Subtraction: When adding or subtracting fractions, finding the LCM of the denominators is crucial to obtain a common denominator.
-
Gear Ratios: In mechanical engineering, gear ratios often involve LCM calculations to determine the optimal gear arrangements for specific speed and torque requirements.
-
Cyclic Events: LCM can help determine when cyclic events coincide, such as planetary alignments or repeating patterns in data analysis.
Advanced Concepts and Extensions
While we've focused on finding the LCM of 4, 5, and 6, the concepts can be extended to larger sets of numbers and even to situations involving rational numbers. More advanced techniques, such as using algorithms based on the Euclidean algorithm for GCD calculation, can improve efficiency when dealing with very large numbers.
Conclusion: Mastering LCM Calculations
Understanding and mastering the calculation of the least common multiple is a valuable skill with wide-ranging applications. The methods outlined in this article – listing multiples, prime factorization, and iterative application of the two-number LCM formula – provide a comprehensive toolkit for solving LCM problems, regardless of the complexity. By choosing the appropriate method based on the numbers involved, one can efficiently and accurately determine the LCM, opening doors to a deeper understanding of mathematical concepts and their real-world applications. Remember, practice makes perfect! Try calculating the LCM of different sets of numbers to solidify your understanding and build your skills.
Latest Posts
Latest Posts
-
The Coefficient Of Determination Is Equal To
Mar 28, 2025
-
The Serum Elisa Test Is Based On Interaction Between
Mar 28, 2025
-
What Is The Lcm Of 3 4 And 8
Mar 28, 2025
-
3 47 Rounded To The Nearest Hundredth
Mar 28, 2025
-
Is A Venus Flytrap More Efective Than Pitcher Plant
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Common Multiple Of 4 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
