Common Factors Of 45 And 30
Juapaving
Mar 26, 2025 · 6 min read
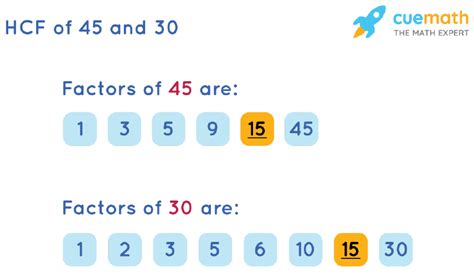
Table of Contents
Unlocking the Secrets of Numbers: A Deep Dive into the Common Factors of 45 and 30
Finding the common factors of two numbers might seem like a simple mathematical task, but understanding the underlying concepts opens doors to a richer appreciation of number theory and its applications. This article will delve into the common factors of 45 and 30, exploring various methods to identify them, understanding their significance, and touching upon related mathematical concepts. We'll move beyond a simple answer and explore the "why" behind the calculations, making this a comprehensive guide for anyone interested in improving their number sense.
What are Factors?
Before we dive into finding the common factors of 45 and 30, let's solidify our understanding of what a factor is. A factor of a number is any whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 45
Let's start by listing all the factors of 45:
- 1: 45 divided by 1 equals 45
- 3: 45 divided by 3 equals 15
- 5: 45 divided by 5 equals 9
- 9: 45 divided by 9 equals 5
- 15: 45 divided by 15 equals 3
- 45: 45 divided by 45 equals 1
Therefore, the factors of 45 are 1, 3, 5, 9, 15, and 45.
Prime Factorization of 45
We can also find the factors of 45 using prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The prime factorization of 45 is 3 x 3 x 5, or 3² x 5. Understanding the prime factorization allows us to easily determine all the factors. Any combination of these prime factors (including 1) will result in a factor of 45.
Finding the Factors of 30
Now, let's list the factors of 30:
- 1: 30 divided by 1 equals 30
- 2: 30 divided by 2 equals 15
- 3: 30 divided by 3 equals 10
- 5: 30 divided by 5 equals 6
- 6: 30 divided by 6 equals 5
- 10: 30 divided by 10 equals 3
- 15: 30 divided by 15 equals 2
- 30: 30 divided by 30 equals 1
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
Prime Factorization of 30
The prime factorization of 30 is 2 x 3 x 5. Again, understanding the prime factorization helps in easily identifying all possible factors.
Identifying Common Factors
Now that we have the factors of both 45 and 30, we can identify the common factors. These are the numbers that appear in both lists:
- 1: Present in both lists.
- 3: Present in both lists.
- 5: Present in both lists.
- 15: Present in both lists.
Therefore, the common factors of 45 and 30 are 1, 3, 5, and 15.
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF), also known as the Highest Common Factor (HCF), is the largest number that divides evenly into both 45 and 30. In this case, the GCF of 45 and 30 is 15.
Finding the GCF using Prime Factorization
The prime factorization method provides an efficient way to find the GCF. Let's look at the prime factorizations again:
- 45 = 3² x 5
- 30 = 2 x 3 x 5
To find the GCF, we identify the common prime factors and take the lowest power of each:
Both numbers share a 3 (to the power of 1) and a 5 (to the power of 1). Therefore, the GCF is 3 x 5 = 15.
Least Common Multiple (LCM)
While we are focusing on common factors, it's worth briefly mentioning the Least Common Multiple (LCM). The LCM is the smallest number that is a multiple of both 45 and 30. This concept is closely related to GCF.
Finding the LCM using Prime Factorization
Using the prime factorizations:
- 45 = 3² x 5
- 30 = 2 x 3 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
The highest power of 2 is 2¹. The highest power of 3 is 3². The highest power of 5 is 5¹. Therefore, the LCM is 2 x 3² x 5 = 90.
Applications of Common Factors and GCF
Understanding common factors and the GCF has practical applications in various areas:
-
Simplifying Fractions: Finding the GCF helps simplify fractions to their lowest terms. For example, the fraction 45/30 can be simplified to 3/2 by dividing both the numerator and the denominator by their GCF, which is 15.
-
Solving Word Problems: Many word problems involve finding the GCF. For example, if you have 45 apples and 30 oranges, and you want to divide them into identical groups, the largest number of groups you can make is 15 (the GCF). Each group will contain 3 apples and 2 oranges.
-
Geometry: The GCF is used in geometry to find the largest square that can tile a rectangle with dimensions equal to the two numbers. For example, a rectangle with sides of 45 and 30 units can be tiled with 15 x 15 squares.
-
Number Theory: Common factors and GCF are fundamental concepts in number theory, a branch of mathematics that studies the properties of numbers.
Beyond the Basics: Exploring Divisibility Rules
Understanding divisibility rules can significantly speed up the process of finding factors. Divisibility rules provide quick ways to determine if a number is divisible by another number without performing long division. For instance:
- Divisibility by 2: A number is divisible by 2 if it's an even number (ends in 0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. (4 + 5 = 9, which is divisible by 3, so 45 is divisible by 3).
- Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
- Divisibility by 10: A number is divisible by 10 if it ends in 0.
By applying these rules, you can quickly identify potential factors and streamline the process of finding common factors and the GCF.
Conclusion: The Significance of Understanding Factors
Finding the common factors of 45 and 30, and understanding the GCF, is more than just a simple mathematical exercise. It’s a gateway to a deeper understanding of number theory, its applications in various fields, and the underlying principles that govern numerical relationships. By mastering these concepts, you're not just learning about factors; you're developing a stronger foundation in mathematics and problem-solving skills that extend far beyond this specific example. The ability to efficiently find factors and the GCF proves invaluable in simplifying calculations, solving complex problems, and appreciating the elegance of mathematical structures. The journey into the world of numbers is a rewarding one, filled with patterns, relationships, and endless opportunities for discovery.
Latest Posts
Latest Posts
-
How Much Cerebral Capacity Do Dolphins Use
Mar 29, 2025
-
The Original Three Components Of The Cell Theory Are That
Mar 29, 2025
-
Give The Temperature And Pressure At Stp
Mar 29, 2025
-
Give The Ground State Electron Configuration For Pb
Mar 29, 2025
-
Worksheet On Simple Compound And Complex Sentences With Answers
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 45 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
