Common Factors Of 3 And 6
Juapaving
Mar 21, 2025 · 5 min read
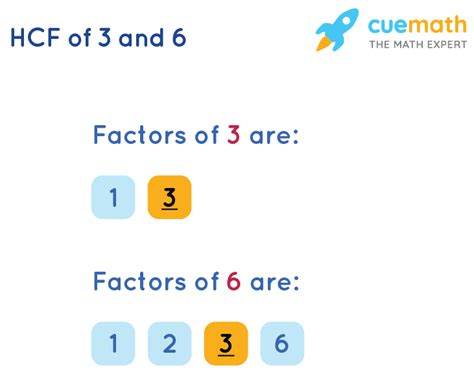
Table of Contents
Unveiling the Common Factors of 3 and 6: A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple task, especially for small numbers like 3 and 6. However, understanding the underlying principles of number theory behind this seemingly simple concept opens doors to a deeper appreciation of mathematics and its applications. This article delves into the common factors of 3 and 6, exploring the concepts of factors, divisors, prime factorization, and their broader implications in mathematics and other fields.
Understanding Factors and Divisors
Before we dive into the specifics of 3 and 6, let's establish a solid foundation. A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, it's a number that can be multiplied by another whole number to produce the original number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
Finding the Factors of 3 and 6
Now, let's identify the factors of 3 and 6 individually:
Factors of 3:
The factors of 3 are surprisingly simple: 1 and 3. 3 is a prime number, meaning its only factors are 1 and itself.
Factors of 6:
The factors of 6 are slightly more numerous: 1, 2, 3, and 6.
Identifying Common Factors
The common factors of two numbers are the numbers that appear in the factor list of both numbers. Comparing the factor lists of 3 and 6, we see that they share the factors 1 and 3. Therefore, the common factors of 3 and 6 are 1 and 3.
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF), also known as the Highest Common Factor (HCF), is the largest number that divides both numbers without leaving a remainder. In the case of 3 and 6, the GCF is 3. This is a crucial concept in various mathematical operations, including simplification of fractions and solving algebraic equations.
Prime Factorization: A Deeper Look
Prime factorization is a fundamental concept in number theory. It involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 3 and 6:
Prime Factorization of 3:
Since 3 is a prime number, its prime factorization is simply 3.
Prime Factorization of 6:
The prime factorization of 6 is 2 x 3.
Using prime factorization to find the GCF involves identifying the common prime factors and multiplying them together. In this case, both 3 and 6 share the prime factor 3. Therefore, the GCF is 3.
Applications of Common Factors and GCF
The concepts of common factors and the GCF extend far beyond basic arithmetic. They find applications in various fields, including:
1. Simplifying Fractions:
The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 6/9 can be simplified by dividing both the numerator (6) and the denominator (9) by their GCF, which is 3. This simplifies the fraction to 2/3.
2. Solving Algebraic Equations:
GCF plays a role in factoring algebraic expressions. For instance, when factoring the expression 3x + 6, we can factor out the GCF of 3, resulting in 3(x + 2).
3. Geometry and Measurement:
GCF is used in solving geometric problems involving area and volume calculations. For example, finding the largest square tile that can perfectly cover a rectangular floor requires finding the GCF of the length and width of the floor.
4. Cryptography:
Prime factorization is the foundation of many modern cryptographic systems. The difficulty of factoring very large numbers into their prime factors forms the basis of the security of these systems.
5. Music Theory:
Interestingly, common factors and GCF also find their way into music theory, particularly in determining intervals and harmonies.
Beyond the Basics: Exploring Further Concepts
The seemingly simple concept of common factors leads to a rich tapestry of mathematical concepts. Let's briefly explore some related ideas:
-
Least Common Multiple (LCM): This is the smallest number that is a multiple of both numbers. For 3 and 6, the LCM is 6. GCF and LCM are related through the formula: GCF(a, b) x LCM(a, b) = a x b.
-
Euclidean Algorithm: This efficient algorithm is used to determine the GCF of two numbers without having to find all their factors.
-
Modular Arithmetic: This branch of number theory deals with remainders after division, and the concepts of factors and GCF are fundamental in this field.
-
Number Theory Theorems: Several theorems in number theory, such as the Fundamental Theorem of Arithmetic (which states that every integer greater than 1 can be uniquely represented as a product of prime numbers), rely heavily on the concepts of factors and prime factorization.
Conclusion: The Significance of Simple Concepts
While finding the common factors of 3 and 6 may appear trivial at first glance, it serves as a gateway to a vast and fascinating world of mathematical concepts. Understanding factors, divisors, prime factorization, GCF, and their applications highlights the power and elegance of number theory and its pervasive influence across diverse fields. The seemingly simple problem of finding the common factors of 3 and 6 demonstrates the beauty of mathematics – how fundamental concepts can underpin complex ideas and real-world applications. The journey from simple observation to a profound understanding of mathematical principles is a rewarding one, showcasing the interconnectedness and utility of even the most elementary mathematical concepts. By understanding these foundational concepts, we can better appreciate the complexity and beauty of the mathematical world around us.
Latest Posts
Latest Posts
-
Is Ice Cream Melting A Physical Change
Mar 27, 2025
-
Why Does Electronegativity Increase From Left To Right
Mar 27, 2025
-
What Is The Lcm Of 25 And 35
Mar 27, 2025
-
What Are All The Factors Of 11
Mar 27, 2025
-
What Is The Factors Of 25
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
