Boyle's Law Describes The Relationship Between
Juapaving
Mar 28, 2025 · 6 min read
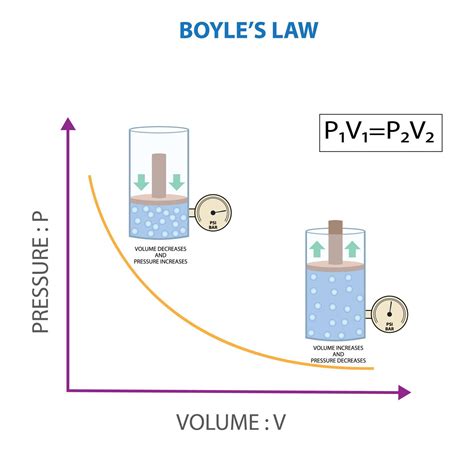
Table of Contents
- Boyle's Law Describes The Relationship Between
- Table of Contents
- Boyle's Law: A Deep Dive into the Relationship Between Pressure and Volume
- The Historical Context: Robert Boyle and the Dawn of Gas Laws
- Experimental Verification: Replicating Boyle's Findings
- Mathematical Representation: The Equation of Boyle's Law
- Units of Measurement: Consistency is Key
- Limitations of Boyle's Law: Beyond Ideal Gases
- Real-World Applications: Boyle's Law in Action
- 1. Scuba Diving and Underwater Activities:
- 2. Meteorology and Weather Forecasting:
- 3. Medical Applications:
- 4. Pneumatic Systems:
- 5. Internal Combustion Engines:
- 6. Aerospace Engineering:
- Beyond the Basics: Connecting Boyle's Law to Other Gas Laws
- Conclusion: The Enduring Legacy of Boyle's Law
- Latest Posts
- Latest Posts
- Related Post
Boyle's Law: A Deep Dive into the Relationship Between Pressure and Volume
Boyle's Law, a cornerstone of gas laws in physics and chemistry, elegantly describes the inverse relationship between the pressure and volume of a gas when temperature is held constant. Understanding this relationship is crucial not only for academic pursuits but also for numerous practical applications across various fields. This comprehensive guide will explore Boyle's Law in detail, covering its historical context, experimental verification, mathematical representation, limitations, and real-world significance.
The Historical Context: Robert Boyle and the Dawn of Gas Laws
Robert Boyle (1627-1691), an influential Irish natural philosopher, chemist, physicist, and inventor, is credited with formulating Boyle's Law. Through meticulous experimentation, primarily using a J-shaped tube filled with mercury and air, Boyle observed a consistent pattern: as he increased the pressure on the trapped air, its volume decreased proportionally. This observation, documented in his groundbreaking work "New Experiments Physico-Mechanicall, Touching the Spring of the Air, and its Effects" (1662), laid the foundation for understanding the behavior of gases. It's important to note that while Boyle is given the credit, similar observations were made independently by Edme Mariotte later in the 17th century, leading to it sometimes being referred to as Boyle-Mariotte Law. However, Boyle's detailed experimental approach and comprehensive documentation cemented his place in scientific history.
Experimental Verification: Replicating Boyle's Findings
While the original J-tube experiment is historically significant, modern demonstrations of Boyle's Law often employ simpler, yet equally effective, methods. A common approach uses a syringe: by compressing the plunger (increasing pressure), you observe a corresponding decrease in the volume of air within the syringe. Conversely, pulling the plunger (decreasing pressure) leads to an increase in volume. These experiments, while visually simple, effectively highlight the inverse relationship. Other methods include using pressure sensors and volume measuring devices attached to sealed containers of gas to obtain precise quantitative data that confirms the law. These experiments are widely used in educational settings to allow students to directly verify the law themselves.
Mathematical Representation: The Equation of Boyle's Law
Boyle's Law is concisely represented by the following mathematical equation:
P₁V₁ = P₂V₂
Where:
- P₁ represents the initial pressure of the gas.
- V₁ represents the initial volume of the gas.
- P₂ represents the final pressure of the gas.
- V₂ represents the final volume of the gas.
This equation demonstrates the inverse proportionality: if the pressure increases, the volume decreases, and vice-versa, while the product of pressure and volume remains constant at a constant temperature. The constancy of P*V is a critical element in understanding and applying the law. This equation serves as a powerful tool for calculating changes in pressure or volume given a change in the other variable, under the condition of constant temperature.
Units of Measurement: Consistency is Key
The accuracy of calculations using Boyle's Law relies heavily on the consistent use of units. Pressure is typically measured in atmospheres (atm), Pascals (Pa), or millimeters of mercury (mmHg). Volume is measured in liters (L), cubic meters (m³), or milliliters (mL). Ensuring that all values in a calculation use the same units is vital to avoid errors. Inconsistent units can lead to significantly inaccurate results.
Limitations of Boyle's Law: Beyond Ideal Gases
Boyle's Law, while incredibly useful, does not perfectly describe the behavior of all gases under all conditions. It's most accurate when applied to ideal gases, which are theoretical gases whose molecules occupy negligible volume and have no intermolecular forces. Real gases, on the other hand, exhibit deviations from ideal behavior, especially at high pressures and low temperatures.
At high pressures, the volume occupied by gas molecules themselves becomes significant, reducing the available free space, thus deviating from the ideal gas assumption. Similarly, at low temperatures, intermolecular forces become more prominent, causing molecules to attract each other and reduce the gas's overall volume.
Therefore, it is crucial to recognize the limitations of Boyle's Law and to consider deviations from ideal behavior when working with real gases under extreme conditions. More sophisticated equations of state, such as the van der Waals equation, better account for these real-world effects.
Real-World Applications: Boyle's Law in Action
Boyle's Law's seemingly simple relationship between pressure and volume has far-reaching applications in a variety of fields:
1. Scuba Diving and Underwater Activities:
Boyle's Law is crucial for scuba divers' safety. As divers descend, the pressure increases, and the volume of air in their lungs decreases. Failure to account for this change in volume can lead to lung injuries or even death. Divers must learn to manage their breathing and adjust their buoyancy accordingly.
2. Meteorology and Weather Forecasting:
Understanding Boyle's Law is essential in weather forecasting and meteorological modeling. Changes in atmospheric pressure directly affect air volume and density, influencing weather patterns and the movement of air masses.
3. Medical Applications:
Boyle's Law principles are used in various medical devices. For example, ventilation systems in hospitals rely on adjusting pressure to regulate the volume of air delivered to patients' lungs.
4. Pneumatic Systems:
Pneumatic systems, which use compressed air to power machinery and tools, heavily depend on Boyle's Law. Understanding the pressure-volume relationship is crucial for designing and operating these systems efficiently and safely.
5. Internal Combustion Engines:
The compression stroke in internal combustion engines exemplifies Boyle's Law. The piston compresses the air-fuel mixture, increasing pressure and decreasing volume before combustion occurs.
6. Aerospace Engineering:
In aerospace engineering, Boyle's law is essential for understanding and designing systems involving gases at varying pressures, such as rocket propulsion and aircraft pressurization systems.
Beyond the Basics: Connecting Boyle's Law to Other Gas Laws
Boyle's Law is just one part of a broader understanding of gas behavior. It's closely related to other gas laws, forming a complete picture of ideal gas behavior:
-
Charles's Law: This law describes the relationship between volume and temperature at constant pressure. Volume increases with increasing temperature and vice versa.
-
Gay-Lussac's Law: This law relates pressure and temperature at constant volume. Pressure increases with increasing temperature and vice versa.
-
The Ideal Gas Law: This combines Boyle's, Charles's, and Gay-Lussac's laws into a single equation (PV = nRT), where 'n' is the number of moles of gas and 'R' is the ideal gas constant. The Ideal Gas Law is a powerful tool for modeling gas behavior under a wide range of conditions.
Understanding the interplay between these laws provides a comprehensive understanding of gas thermodynamics and its diverse applications.
Conclusion: The Enduring Legacy of Boyle's Law
Boyle's Law, while initially a simple observation, has evolved into a fundamental principle in physics and chemistry. Its applications extend far beyond the laboratory, influencing numerous technologies and shaping our understanding of the world around us. From the depths of the ocean to the heights of the atmosphere, the inverse relationship between pressure and volume continues to play a critical role in various fields. By grasping the principles of Boyle's Law and its connection to other gas laws, we unlock a deeper understanding of the behavior of gases and their vital role in our daily lives. The ongoing relevance of Boyle's work underscores the enduring power of meticulous experimentation and insightful observation in scientific discovery.
Latest Posts
Latest Posts
-
Metals That Can Be Cut With Knife
Apr 02, 2025
-
Magnetic Field From A Current Loop
Apr 02, 2025
-
Collection Of Nerve Cell Bodies Outside The Cns
Apr 02, 2025
-
What Do Nitrification And Denitrification Have In Common
Apr 02, 2025
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Boyle's Law Describes The Relationship Between . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
