As The Temperature Of A Gas Increases
Juapaving
Mar 28, 2025 · 5 min read
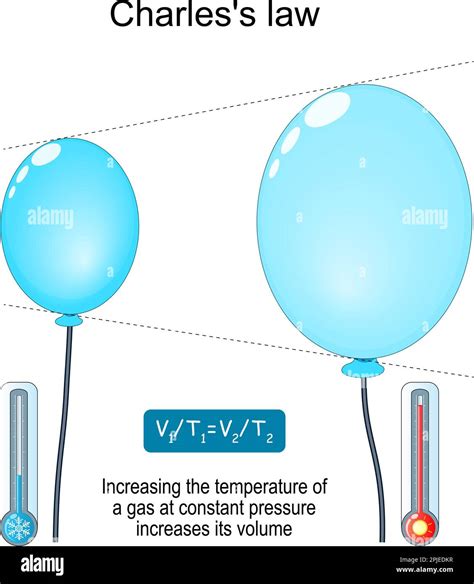
Table of Contents
As the Temperature of a Gas Increases: Exploring the Kinetic Molecular Theory and its Implications
The behavior of gases is a fascinating area of study, with countless applications in our daily lives and advanced technologies. Understanding how gases respond to changes in temperature, pressure, and volume is crucial in fields ranging from meteorology and aerospace engineering to chemistry and material science. This article delves into the effects of increasing the temperature of a gas, focusing on the underlying principles of the Kinetic Molecular Theory and its various implications.
The Kinetic Molecular Theory: A Foundation for Understanding Gaseous Behavior
At the heart of understanding gas behavior lies the Kinetic Molecular Theory (KMT). This theory posits that gases are composed of a vast number of tiny particles (atoms or molecules) that are in constant, random motion. These particles are considered to be point masses, meaning their volume is negligible compared to the volume of the container they occupy. Furthermore, the KMT assumes that:
- Collisions are elastic: When particles collide with each other or the container walls, there's no net loss of kinetic energy.
- Forces of attraction and repulsion are negligible: The particles are assumed to interact very weakly, if at all, with each other.
- Average kinetic energy is proportional to absolute temperature: This is a cornerstone of the KMT; the higher the temperature, the faster the particles move, and vice versa.
The Impact of Increasing Temperature: A Deeper Dive
When you increase the temperature of a gas, you directly increase the average kinetic energy of its constituent particles. This translates to several observable and measurable effects:
1. Increased Particle Speed and Frequency of Collisions
The most immediate consequence is an increase in the average speed of the gas particles. As kinetic energy is directly proportional to the square of velocity (KE = 1/2mv²), a higher temperature means particles move faster. This leads to a higher frequency of collisions between particles and between particles and the container walls.
2. Increased Pressure
The increased frequency and force of collisions with the container walls translates to a higher pressure. This is because pressure is defined as the force exerted per unit area. More frequent and forceful collisions mean a greater force exerted on the walls, resulting in an increased pressure. This relationship is famously described by Gay-Lussac's Law, which states that at constant volume, the pressure of a gas is directly proportional to its absolute temperature.
3. Increased Volume (at constant pressure)
If the gas is allowed to expand, meaning the pressure remains constant, the increased kinetic energy will cause the gas to occupy a larger volume. This is because the faster-moving particles will push against the container walls with greater force, causing the volume to increase until a new equilibrium is reached where the pressure remains constant. This relationship is illustrated by Charles's Law, which states that at constant pressure, the volume of a gas is directly proportional to its absolute temperature.
4. Changes in Density
As the temperature increases and the volume expands (at constant pressure), the density of the gas decreases. Density is mass per unit volume, and if the volume increases while the mass remains constant, the density must decrease. This explains why hot air rises; it's less dense than the surrounding cooler air.
5. Increased Rate of Diffusion and Effusion
Higher temperatures lead to faster-moving particles, which consequently results in a faster rate of diffusion and effusion. Diffusion refers to the mixing of gases, while effusion refers to the passage of a gas through a small hole. Faster particles will cover more ground in a given time, leading to faster diffusion and effusion rates. Graham's Law of Effusion quantifies this relationship, stating that the rate of effusion is inversely proportional to the square root of the molar mass of the gas.
6. Changes in Reaction Rates (in Chemical Reactions)
In chemical reactions involving gases, increasing the temperature often leads to a significant increase in the reaction rate. This is because a higher temperature means a greater proportion of molecules possess sufficient energy (activation energy) to overcome the energy barrier required for the reaction to occur. This is explained by the Arrhenius equation, which shows the relationship between reaction rate, temperature, and activation energy.
Real-World Applications and Examples
The principles discussed above have widespread applications in various fields:
- Meteorology: Understanding how temperature affects air pressure and volume is critical for weather forecasting and predicting atmospheric phenomena like thunderstorms and hurricanes.
- Aerospace Engineering: Designing aircraft and rockets requires a thorough understanding of gas behavior at varying temperatures and pressures.
- Automotive Industry: The operation of internal combustion engines relies heavily on the principles of gas expansion and compression at different temperatures.
- Refrigeration and Air Conditioning: These technologies exploit the relationship between temperature and pressure in refrigerants to achieve cooling effects.
- Chemical Engineering: Industrial chemical processes often involve gases at various temperatures, and a precise understanding of gas behavior is crucial for efficient and safe operation.
- Medical Applications: Gas behavior principles are relevant in various medical technologies, including respiratory therapy and anesthesia.
Beyond Ideal Gases: Deviations from the Kinetic Molecular Theory
The KMT provides a useful model for understanding gas behavior, but it's crucial to acknowledge its limitations. Real gases deviate from ideal behavior under certain conditions, particularly at high pressures and low temperatures. At high pressures, the volume of the gas particles becomes significant compared to the container volume, and intermolecular forces become more prominent. At low temperatures, intermolecular forces become stronger, leading to significant deviations from ideal behavior. More sophisticated models, such as the van der Waals equation, are necessary to accurately describe the behavior of real gases under these conditions.
Conclusion: Temperature's Crucial Role in Gaseous Systems
The temperature of a gas plays a profoundly important role in determining its behavior. As the temperature increases, the kinetic energy of gas particles increases, leading to a range of observable effects including increased pressure, volume (at constant pressure), diffusion rate, and reaction rates in chemical processes. While the Kinetic Molecular Theory provides a solid foundation for understanding these relationships, it's essential to recognize the limitations of the ideal gas model and consider the deviations exhibited by real gases under specific conditions. The implications of this understanding are vast, impacting various scientific and engineering disciplines and shaping our everyday experiences. Further research continues to refine our understanding of gas behavior, pushing the boundaries of technology and scientific discovery.
Latest Posts
Latest Posts
-
Adjectives That Start With The Letter C
Mar 31, 2025
-
Lcm Of 9 And 12 And 15
Mar 31, 2025
-
Which Of The Following Processes Returns Carbon To The Atmosphere
Mar 31, 2025
-
5 Letter Word That Starts With Vi
Mar 31, 2025
-
Can Acquired Characteristics Be Passed On The Next Generation
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about As The Temperature Of A Gas Increases . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
