Are The Diagonals Of An Isosceles Trapezoid Congruent
Juapaving
Mar 28, 2025 · 6 min read
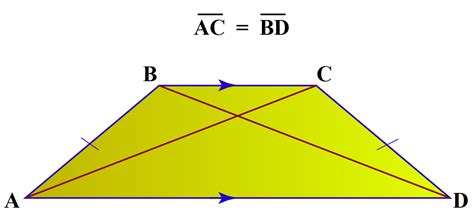
Table of Contents
Are the Diagonals of an Isosceles Trapezoid Congruent? A Comprehensive Exploration
The question of whether the diagonals of an isosceles trapezoid are congruent is a fundamental concept in geometry. While it might seem intuitive, a rigorous understanding requires a deep dive into the properties of isosceles trapezoids and the application of geometric theorems. This article will explore this question in detail, providing a comprehensive analysis with proofs and related discussions. We'll unpack the definition of an isosceles trapezoid, examine relevant theorems, and ultimately answer the question definitively. We'll also explore related concepts and applications.
Understanding Isosceles Trapezoids
Before we delve into the congruency of diagonals, let's clearly define an isosceles trapezoid. A trapezoid (or trapezium, depending on regional terminology) is a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases, and the other two sides are called the legs. An isosceles trapezoid is a special type of trapezoid where the two legs are congruent (equal in length). This seemingly small distinction leads to a number of unique properties.
Key Properties of Isosceles Trapezoids
Isosceles trapezoids possess several characteristic properties that distinguish them from other trapezoids:
-
Base Angles are Congruent: The base angles of an isosceles trapezoid are congruent. This means that the two angles adjacent to each base are equal in measure. For example, if we label the bases AB and CD, then ∠DAB ≅ ∠ABC and ∠ADC ≅ ∠BCD.
-
Diagonals are Congruent: This is the core question of this article, and we will prove this property shortly. The diagonals of an isosceles trapezoid are equal in length.
-
Symmetry: Isosceles trapezoids exhibit a certain symmetry. If you were to draw a line perpendicular to both bases, connecting their midpoints, this line would be a line of symmetry.
-
Circumscribable: An isosceles trapezoid can be inscribed in a circle. This means that a circle can be drawn that passes through all four vertices of the trapezoid. This property is a direct consequence of the congruent base angles.
Proving the Congruence of Diagonals
Now, let's tackle the main question: are the diagonals of an isosceles trapezoid congruent? The answer is yes. We can prove this using various methods. Here, we'll present a proof using congruent triangles.
Theorem: The diagonals of an isosceles trapezoid are congruent.
Proof:
Consider an isosceles trapezoid ABCD, where AB || CD and AD ≅ BC. Let AC and BD be the diagonals. We want to prove that AC ≅ BD.
-
Construct: Draw altitudes from A and B to CD, meeting CD at points E and F respectively.
-
Congruent Triangles: Consider triangles ADE and BCF. We know that:
- AD ≅ BC (given, definition of isosceles trapezoid)
- ∠AED ≅ ∠BFC (both are right angles, due to the construction of altitudes)
- AE ≅ BF (since ABCD is an isosceles trapezoid, the altitudes from A and B to the base CD are congruent, and the distance between parallel lines are constant)
-
Congruence: By the Hypotenuse-Leg (HL) theorem (a specific case of the Pythagorean theorem applicable to right-angled triangles), triangles ADE and BCF are congruent (ΔADE ≅ ΔBCF).
-
Congruent Segments: Since ΔADE ≅ ΔBCF, we have DE ≅ CF.
-
Segment Addition: We can express the lengths of the diagonals as:
- AC = AE + EC
- BD = BF + FD
Since AE ≅ BF (proven above) and EC ≅ FD (from DE ≅ CF and ED + DC = FC + DC, implying EC = FD), we can substitute these congruencies to get AC = BD.
-
Conclusion: Therefore, AC ≅ BD. The diagonals of the isosceles trapezoid are congruent.
Alternative Proof Using Vector Geometry
A more advanced proof can be constructed using vector geometry. This approach offers a different perspective and utilizes vector properties to demonstrate diagonal congruency.
Let's represent the vertices of the isosceles trapezoid ABCD using vectors: A = a, B = b, C = c, D = d.
Since AB is parallel to CD, the vector AB (b - a) is parallel to the vector CD (c - d). In an isosceles trapezoid, AD = BC. Therefore, the vector AD (d - a) = the vector BC (c - b).
The diagonals AC and BD can be represented by vectors:
- AC = c - a
- BD = d - b
To prove congruency, we need to show that the magnitudes of these vectors are equal: |c - a| = |d - b|. This proof requires manipulation of vector equations and involves leveraging the properties of parallel vectors and congruent legs. Due to its complexity, a detailed vector proof is beyond the scope of this introductory article, but the interested reader can find such proofs in more advanced geometry texts.
Applications and Further Exploration
The property of congruent diagonals in an isosceles trapezoid finds applications in various areas:
-
Construction and Engineering: Understanding the properties of isosceles trapezoids is essential in structural design and construction, ensuring stability and symmetry in building structures.
-
Computer Graphics: In computer graphics and image processing, isosceles trapezoids are used in transformations and projections. The knowledge of their diagonals plays a vital role in accurate calculations.
-
Tessellations: Isosceles trapezoids, along with other geometric shapes, can be used to create various tessellations (tilings) of the plane. Understanding their properties helps in designing intricate and aesthetically pleasing patterns.
-
Advanced Geometry: The properties of isosceles trapezoids form a foundation for exploring more complex geometric concepts such as cyclic quadrilaterals and their properties.
Related Concepts and Theorems
Several other geometric theorems and concepts are closely related to isosceles trapezoids and their diagonals:
-
Ptolemy's Theorem: This theorem deals with cyclic quadrilaterals (quadrilaterals that can be inscribed in a circle). Since an isosceles trapezoid is a cyclic quadrilateral, Ptolemy's theorem can be applied, albeit with a slightly different interpretation due to the parallel sides.
-
Midline Theorem: The midline theorem states that the segment connecting the midpoints of the legs of a trapezoid is parallel to the bases and half the sum of their lengths. This theorem can be applied to isosceles trapezoids, leading to interesting relationships between the midsegment and the bases.
-
Area of an Isosceles Trapezoid: The area of an isosceles trapezoid can be calculated using the formula: Area = (1/2)(sum of bases)(height). Understanding the height and the relationship between bases and diagonals contributes to calculating the area accurately.
Conclusion
In conclusion, the diagonals of an isosceles trapezoid are indeed congruent. We have demonstrated this through a rigorous geometric proof using congruent triangles and briefly touched upon an alternative vector-based approach. This fundamental property has implications across various fields, from architecture and engineering to advanced mathematics and computer graphics. The exploration of isosceles trapezoids provides a valuable opportunity to deepen our understanding of geometric principles and their applications in the real world. Further exploration into related theorems and concepts can lead to a richer and more complete understanding of geometry.
Latest Posts
Latest Posts
-
Equation Of A Circle Calculator Given Two Points
Mar 31, 2025
-
What Is The Least Common Denominator Of 8 And 12
Mar 31, 2025
-
5 Letter Words With Er In The End
Mar 31, 2025
-
What Are The Common Factors Of 28 And 36
Mar 31, 2025
-
What Is 6 10 As A Percentage
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Are The Diagonals Of An Isosceles Trapezoid Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
