All Of The Properties In Math
Juapaving
Mar 26, 2025 · 7 min read
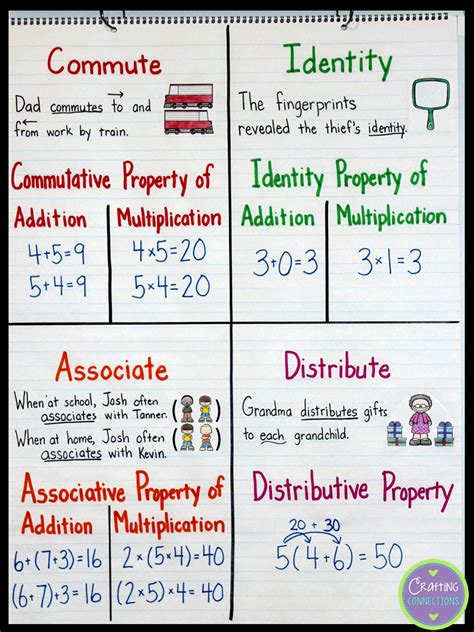
Table of Contents
All the Properties in Math: A Comprehensive Guide
Mathematics, at its core, is a study of patterns, structures, and relationships. Underlying these studies are fundamental properties, axioms, and theorems that govern how mathematical objects behave and interact. Understanding these properties is crucial for mastering mathematical concepts, from basic arithmetic to advanced calculus and beyond. This comprehensive guide explores a wide range of mathematical properties, categorized for clarity and ease of understanding.
Number Properties
The foundation of mathematics rests on the properties of numbers. These properties dictate how numbers behave under various operations like addition, subtraction, multiplication, and division. Let's delve into some key number properties:
1. Closure Property
The closure property states that performing a specific operation on two numbers within a set always results in another number within that same set.
- Addition: The sum of two real numbers is always a real number. For example, 2 + 3 = 5 (both 2, 3, and 5 are real numbers).
- Subtraction: The difference between two real numbers is always a real number. 5 - 2 = 3.
- Multiplication: The product of two real numbers is always a real number. 2 x 3 = 6.
- Division: The division of two real numbers is always a real number except when the divisor is zero. Division by zero is undefined.
Note: Closure doesn't always hold true for all sets and operations. For example, the set of positive integers is not closed under subtraction (e.g., 2 - 5 = -3, which is not a positive integer).
2. Commutative Property
The commutative property asserts that the order of operands in an operation doesn't affect the result.
- Addition: a + b = b + a (e.g., 2 + 3 = 3 + 2 = 5)
- Multiplication: a x b = b x a (e.g., 2 x 3 = 3 x 2 = 6)
Note: Subtraction and division are not commutative. 2 - 3 ≠ 3 - 2 and 2 ÷ 3 ≠ 3 ÷ 2.
3. Associative Property
The associative property states that the grouping of operands in an operation doesn't affect the result.
- Addition: (a + b) + c = a + (b + c) (e.g., (2 + 3) + 4 = 2 + (3 + 4) = 9)
- Multiplication: (a x b) x c = a x (b x c) (e.g., (2 x 3) x 4 = 2 x (3 x 4) = 24)
Note: Subtraction and division are not associative. (2 - 3) - 4 ≠ 2 - (3 - 4) and (2 ÷ 3) ÷ 4 ≠ 2 ÷ (3 ÷ 4).
4. Distributive Property
The distributive property connects multiplication and addition (or subtraction). It states that multiplying a number by a sum (or difference) is the same as multiplying the number by each term in the sum (or difference) and then adding (or subtracting) the products.
- Distributive over Addition: a x (b + c) = (a x b) + (a x c) (e.g., 2 x (3 + 4) = (2 x 3) + (2 x 4) = 14)
- Distributive over Subtraction: a x (b - c) = (a x b) - (a x c) (e.g., 2 x (4 - 3) = (2 x 4) - (2 x 3) = 2)
5. Identity Property
The identity property states that there exists a specific element (identity element) within a set that, when operated upon with another element, leaves the other element unchanged.
- Additive Identity: 0. a + 0 = a (e.g., 5 + 0 = 5)
- Multiplicative Identity: 1. a x 1 = a (e.g., 5 x 1 = 5)
6. Inverse Property
The inverse property states that for every element in a set, there exists another element (inverse element) that, when operated upon with the original element, results in the identity element.
- Additive Inverse: -a. a + (-a) = 0 (e.g., 5 + (-5) = 0)
- Multiplicative Inverse: 1/a (for a ≠ 0). a x (1/a) = 1 (e.g., 5 x (1/5) = 1)
Properties of Equations and Inequalities
Equations and inequalities are fundamental tools in mathematics used to represent relationships between variables and constants. Several properties govern how we manipulate equations and inequalities to solve them.
1. Reflexive Property
The reflexive property states that a quantity is equal to itself. This is often represented as:
- a = a
2. Symmetric Property
The symmetric property states that if a = b, then b = a.
3. Transitive Property
The transitive property states that if a = b and b = c, then a = c. This applies to inequalities as well: if a < b and b < c, then a < c.
4. Addition Property of Equality
If a = b, then a + c = b + c. You can add the same quantity to both sides of an equation without changing the equality.
5. Subtraction Property of Equality
If a = b, then a - c = b - c. You can subtract the same quantity from both sides of an equation without changing the equality.
6. Multiplication Property of Equality
If a = b, then a x c = b x c. You can multiply both sides of an equation by the same non-zero quantity without changing the equality.
7. Division Property of Equality
If a = b, and c ≠ 0, then a ÷ c = b ÷ c. You can divide both sides of an equation by the same non-zero quantity without changing the equality.
Properties in Geometry
Geometry deals with shapes, sizes, relative positions of figures, and the properties of space. Several key properties govern geometric figures and their relationships.
1. Properties of Triangles
- Angle Sum Property: The sum of angles in any triangle is always 180 degrees.
- Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the angles opposite those sides are congruent.
- Pythagorean Theorem: In a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (a² + b² = c²).
2. Properties of Quadrilaterals
Various quadrilaterals (four-sided polygons) have unique properties:
- Rectangle: Opposite sides are parallel and equal, all angles are 90 degrees.
- Square: All sides are equal, all angles are 90 degrees.
- Parallelogram: Opposite sides are parallel and equal.
- Rhombus: All sides are equal.
- Trapezoid: At least one pair of opposite sides are parallel.
3. Properties of Circles
- Circumference: The distance around a circle, calculated as 2πr (where r is the radius).
- Area: The space enclosed within a circle, calculated as πr².
- Diameter: The distance across a circle through the center (twice the radius).
Properties in Set Theory
Set theory deals with collections of objects called sets. Several properties define how sets behave and interact:
1. Union
The union of two sets A and B (denoted A ∪ B) is the set containing all elements that are in A or in B or in both.
2. Intersection
The intersection of two sets A and B (denoted A ∩ B) is the set containing all elements that are in both A and B.
3. Complement
The complement of a set A (denoted A') is the set containing all elements that are not in A.
4. Subset
A set A is a subset of set B (denoted A ⊆ B) if all elements of A are also elements of B.
5. Power Set
The power set of a set A (denoted P(A)) is the set of all possible subsets of A, including the empty set and A itself.
Properties in Linear Algebra
Linear algebra deals with vector spaces, linear transformations, and systems of linear equations. Key properties include:
1. Linearity
Linear transformations preserve vector addition and scalar multiplication. This is a fundamental property in linear algebra.
2. Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are essential concepts used to analyze linear transformations. Eigenvectors remain unchanged in direction when subjected to a linear transformation, and the eigenvalue represents the scaling factor.
3. Properties of Matrices
Matrices have various properties, including:
- Transpose: Switching rows and columns.
- Inverse: A matrix that, when multiplied by the original matrix, results in the identity matrix.
- Determinant: A scalar value associated with a square matrix.
This extensive guide provides a solid foundation in understanding various mathematical properties. Each area – number properties, equation properties, geometric properties, set theory properties, and linear algebra properties – is rich with further exploration and nuances. Remember that mastering these properties is fundamental to progressing in your mathematical journey, enabling you to solve complex problems and delve into more advanced concepts with confidence. Further study in specific areas will reveal even more intricate and fascinating properties within the vast and ever-evolving field of mathematics.
Latest Posts
Latest Posts
-
What Is The Lcm Of 5 6 And 7
Mar 29, 2025
-
How Much Valence Electrons Does Oxygen Have
Mar 29, 2025
-
What Percent Of 80 Is 12
Mar 29, 2025
-
Least Common Multiple Of 6 7 And 8
Mar 29, 2025
-
What Is 7 8 Expressed As A Percent
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about All Of The Properties In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
