A Frequency Polygon Is Graphed Using
Juapaving
Apr 05, 2025 · 5 min read
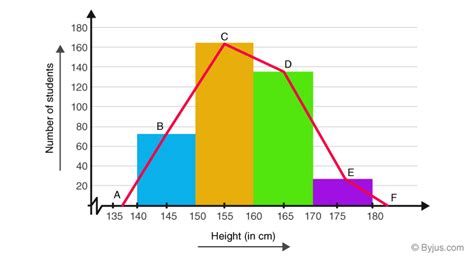
Table of Contents
A Frequency Polygon is Graphed Using: A Comprehensive Guide
A frequency polygon is a powerful visual tool used in statistics to represent the frequency distribution of a dataset. Unlike histograms which use bars, frequency polygons utilize lines to connect points representing the frequency of each class interval. Understanding how to construct and interpret a frequency polygon is crucial for analyzing data and drawing meaningful conclusions. This comprehensive guide will delve into the process of creating a frequency polygon, highlighting key steps and considerations.
Understanding the Components of a Frequency Polygon
Before diving into the construction process, let's familiarize ourselves with the essential components of a frequency polygon:
-
Class Intervals: These are the ranges of values within your data. For example, if you're analyzing test scores, your class intervals might be 0-10, 11-20, 21-30, and so on. The width of these intervals should ideally be consistent for accurate representation.
-
Frequencies: This represents the number of data points falling within each class interval. If 5 students scored between 0 and 10, the frequency for that interval is 5.
-
Midpoints: Each class interval has a midpoint. This is calculated by averaging the lower and upper limits of the interval. For the interval 0-10, the midpoint is (0+10)/2 = 5. Midpoints are plotted on the x-axis of the frequency polygon.
-
Frequency Values: These are plotted on the y-axis, representing the frequency corresponding to each midpoint.
Step-by-Step Guide to Constructing a Frequency Polygon
Creating a frequency polygon involves several key steps:
1. Organize your Data: Begin by organizing your raw data into a frequency distribution table. This table will list the class intervals, their corresponding frequencies, and the calculated midpoints.
Example: Let's say we have the following data representing the heights (in centimeters) of 30 students:
150, 155, 160, 162, 165, 168, 170, 172, 175, 175, 178, 180, 180, 182, 185, 185, 188, 190, 190, 192, 195, 195, 198, 200, 200, 202, 205, 205, 208, 210
We can organize this into a frequency distribution table with class intervals of 10 cm:
| Class Interval (cm) | Frequency (f) | Midpoint (x) |
|---|---|---|
| 150-159 | 2 | 154.5 |
| 160-169 | 4 | 164.5 |
| 170-179 | 5 | 174.5 |
| 180-189 | 6 | 184.5 |
| 190-199 | 6 | 194.5 |
| 200-209 | 5 | 204.5 |
| 210-219 | 2 | 214.5 |
2. Draw the Axes: Create a Cartesian coordinate system. The horizontal axis (x-axis) will represent the midpoints of the class intervals, and the vertical axis (y-axis) will represent the frequencies. Ensure your axes are appropriately scaled to accommodate your data range.
3. Plot the Points: For each class interval, plot a point on the graph corresponding to its midpoint (x-axis) and its frequency (y-axis).
4. Connect the Points: Connect the plotted points with straight lines. This forms the frequency polygon.
5. Extend the Polygon: To complete the polygon, extend the lines to the x-axis at both ends. The first line connects the first plotted point to a point on the x-axis at the midpoint of the class interval before the first. The last line connects the final plotted point to a point on the x-axis at the midpoint of the class interval after the last. This ensures the polygon is closed.
Interpreting a Frequency Polygon
Once constructed, the frequency polygon provides valuable insights into the data's distribution:
-
Central Tendency: The peak of the polygon generally indicates the central tendency of the data. A symmetrical polygon suggests a balanced distribution, while a skewed polygon reveals a concentration of data towards one end.
-
Spread: The width of the polygon reflects the spread or dispersion of the data. A wide polygon indicates high variability, whereas a narrow polygon suggests low variability.
-
Shape: The shape of the polygon can reveal important patterns in the data, such as normality (bell-shaped), bimodality (two peaks), or other unique characteristics.
-
Comparison: Frequency polygons are particularly useful for comparing different datasets. By plotting multiple polygons on the same graph, you can visually assess the similarities and differences in their distributions.
Frequency Polygon vs. Histogram: Key Differences
While both frequency polygons and histograms represent frequency distributions, they have key differences:
| Feature | Frequency Polygon | Histogram |
|---|---|---|
| Representation | Uses lines to connect points | Uses bars to represent frequencies |
| Midpoints | Uses midpoints of class intervals | Uses class boundaries |
| Visual Appeal | Shows the shape of distribution more clearly | Shows the frequency for each interval directly |
| Comparison | Excellent for comparing multiple distributions | Less effective for comparing multiple distributions |
Advanced Applications and Considerations
Frequency polygons are not limited to basic data analysis. They find application in diverse fields including:
-
Quality Control: Monitoring process variability and identifying outliers.
-
Market Research: Analyzing customer preferences and trends.
-
Environmental Science: Studying pollutant concentrations and climate patterns.
-
Healthcare: Analyzing patient demographics and health outcomes.
Several considerations enhance the accuracy and interpretability of a frequency polygon:
-
Choice of Class Intervals: Selecting appropriate class intervals is critical. Too few intervals might obscure important details, while too many might create a jagged and uninformative polygon. Strive for a balance that accurately reflects the data's structure.
-
Scale and Labeling: Clear and consistent axis labeling and scaling are essential for accurate interpretation. Units should be clearly indicated, and the axes should be scaled to effectively represent the data range.
-
Software Tools: Statistical software packages (e.g., SPSS, R, Excel) provide tools to automatically generate frequency polygons, freeing you to focus on analysis and interpretation.
Conclusion
A frequency polygon is a valuable statistical tool offering a visually compelling way to represent frequency distributions. By following the steps outlined above and considering the points discussed, you can effectively construct and interpret frequency polygons to gain insights from your data. Remember that accurate data organization, appropriate scaling, and thoughtful interpretation are key to extracting meaningful conclusions from your frequency polygon analysis. This comprehensive understanding allows you to leverage the power of this visual tool for effective data analysis and informed decision-making in various fields. The ability to compare multiple frequency polygons further enhances the analytical capabilities of this method, making it a staple in data visualization and statistical interpretation.
Latest Posts
Latest Posts
-
A Pectoral Girdle Consists Of Two Bones The And The
Apr 05, 2025
-
How Many Feet Is 26 Inches
Apr 05, 2025
-
Actin And Myosin Are What Type Of Biological Molecule
Apr 05, 2025
-
Fluid Part Of Blood After Removal Of Corpuscles Is
Apr 05, 2025
-
Is A Substance In Which Another Substance Is Dissolved
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about A Frequency Polygon Is Graphed Using . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
