A Chord That Passes Through The Center Of The Circle
Juapaving
Mar 28, 2025 · 6 min read
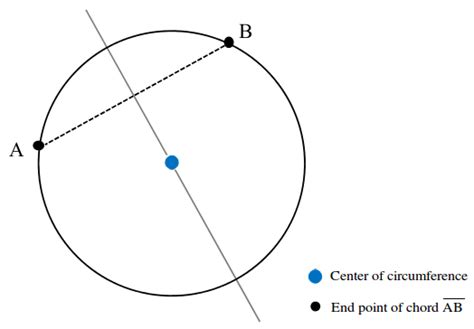
Table of Contents
A Chord That Passes Through the Center: Exploring the Properties of a Diameter
A seemingly simple concept in geometry, the chord that passes through the circle's center holds a significant position, possessing unique properties and playing a crucial role in various geometric theorems and applications. This chord, known as the diameter, is more than just a line segment connecting two points on the circle; it's a fundamental element that defines the circle's characteristics and facilitates the exploration of its intricate relationships with other geometric figures. This article delves into the properties of a diameter, its relationship to other elements within the circle, and its applications in various fields.
Understanding the Diameter: Definition and Key Properties
A diameter is defined as a chord that passes through the center of a circle. It's the longest chord possible within a circle. This seemingly simple definition unlocks a wealth of geometric insights. Let's break down some of its key properties:
1. Relationship to the Radius:
The diameter's most fundamental property is its direct relationship with the radius. The radius is a line segment connecting the center of the circle to any point on the circle. The diameter is precisely twice the length of the radius. This simple relationship is crucial for numerous calculations involving circles. If you know the radius, you instantly know the diameter, and vice versa.
2. Dividing the Circle:
A diameter divides the circle into two semicircles. These semicircles are congruent, meaning they have identical size and shape. This property simplifies several geometrical problems, allowing for symmetrical analysis and calculations.
3. Perpendicular Bisector of Chords:
A diameter that is perpendicular to a chord bisects that chord. This means the diameter cuts the chord into two equal halves. Conversely, if a chord is bisected by a diameter, the diameter is perpendicular to the chord. This property proves invaluable when dealing with chord lengths and distances within the circle.
4. Angle Subtended at the Circumference:
Any angle subtended by a diameter at the circumference of the circle is a right angle (90 degrees). This theorem, a cornerstone of circle geometry, provides a powerful tool for solving problems involving angles and triangles inscribed within a circle. This relationship is used extensively in various proofs and constructions.
5. Applications in Trigonometry:
The diameter plays a crucial role in trigonometry, particularly in the unit circle. The unit circle, a circle with a radius of 1, serves as a fundamental tool for understanding trigonometric functions. The diameter of the unit circle provides a visual representation of the range of sine and cosine functions, which oscillate between -1 and 1.
Exploring the Diameter's Relationship with Other Circle Elements
The diameter's unique properties allow for a deeper understanding of other elements within the circle, including chords, tangents, and arcs.
1. Relationship with Chords:
As previously mentioned, the diameter's relationship with chords is fundamental. The perpendicular bisector property simplifies calculations related to chord lengths and distances. This is particularly useful in problems involving intersecting chords or chords and tangents.
2. Relationship with Tangents:
A tangent to a circle is a line that touches the circle at exactly one point. The diameter plays a vital role in finding the length of tangents drawn from an external point to the circle. The distance from the external point to the point of tangency can be related to the radius and the distance from the external point to the center of the circle, ultimately involving the diameter.
3. Relationship with Arcs and Sectors:
The diameter divides the circle's circumference into two equal arcs, each representing a semicircle. Similarly, it divides the circle's area into two equal sectors. Understanding this division is important when calculating arc lengths, sector areas, and segment areas.
4. Inscribed Angles and Cyclic Quadrilaterals:
The diameter's role in defining right angles subtended at the circumference extends to other geometrical figures inscribed within the circle. Understanding inscribed angles and cyclic quadrilaterals heavily relies on the diameter and its properties. For instance, the angle subtended by the diameter at the circumference is always 90 degrees, a key element in proving theorems related to cyclic quadrilaterals.
Applications of the Diameter in Real-World Scenarios
The concept of the diameter isn't confined to theoretical geometry; it finds practical applications in numerous fields:
1. Engineering and Design:
Engineers use the properties of the diameter extensively in designing circular structures, such as wheels, pipes, gears, and other mechanical components. Calculations involving circumference, area, and other parameters heavily rely on the diameter.
2. Architecture and Construction:
Circular designs are frequently used in architecture, from domes to arches. The diameter plays a crucial role in determining the size, strength, and stability of these structures. Architects and structural engineers utilize diameter calculations for precise design and construction.
3. Manufacturing and Production:
In manufacturing processes, the diameter is a critical measurement for various components. Precision manufacturing requires accurate diameter measurements for quality control and to ensure proper functionality of components.
4. Astronomy and Cosmology:
The concept of diameter extends to celestial bodies, such as planets and stars. Astronomers use diameter measurements to estimate the size and physical properties of these astronomical objects. Understanding the diameter of celestial bodies contributes significantly to our understanding of the universe.
Advanced Concepts and Theorems Involving the Diameter
Beyond its fundamental properties, the diameter features prominently in more advanced geometric concepts and theorems:
1. Ptolemy's Theorem:
Ptolemy's Theorem, a significant result in geometry, relates the lengths of the sides and diagonals of a cyclic quadrilateral. This theorem, which is closely tied to the properties of inscribed angles and the diameter, finds applications in various geometric problems.
2. Power of a Point Theorem:
The power of a point theorem describes the relationship between the lengths of segments formed by intersecting lines and the circle. The diameter plays a role in the specific cases of this theorem, particularly when dealing with intersecting chords or tangents.
3. Circle Inversion:
Circle inversion is a geometric transformation that maps points and lines in the plane to their corresponding counterparts, often involving the diameter and the circle's radius in the mapping process.
Conclusion: The Diameter's Enduring Importance in Geometry
The diameter, seemingly a simple concept, is far more significant than it initially appears. Its fundamental properties underpin numerous geometrical theorems and have far-reaching applications in various fields. From engineering and design to astronomy and cosmology, understanding the diameter and its relationship with other elements within a circle is essential for solving problems and understanding the world around us. Its enduring importance in geometry underscores its role as a cornerstone of this fundamental branch of mathematics. The diameter is not merely a line; it is a key to unlocking a wealth of geometric understanding and applications. Its properties offer a powerful toolkit for tackling complex geometrical problems and contribute significantly to our understanding of shapes and spaces. Further exploration of the diameter's properties and related theorems will continue to yield new insights and applications in the years to come.
Latest Posts
Latest Posts
-
What Type Of Heat Transfer Is Boiling Water
Mar 31, 2025
-
Lcm Of 5 3 And 6
Mar 31, 2025
-
In Which Hemisphere India Is Located
Mar 31, 2025
-
Worksheet On Passive And Active Voice
Mar 31, 2025
-
A Piece Of Land Surrounded By Water On Three Sides
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about A Chord That Passes Through The Center Of The Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
