Lcm Of 5 3 And 6
Juapaving
Mar 31, 2025 · 5 min read
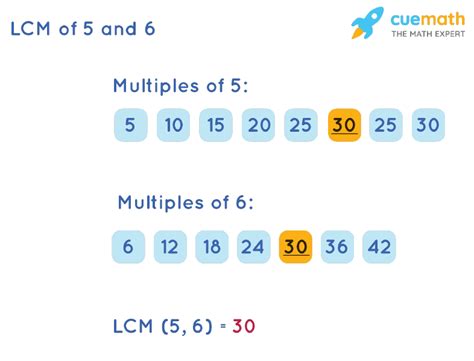
Table of Contents
Finding the LCM of 5, 3, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications in various fields. This article delves into the process of calculating the LCM of 5, 3, and 6, providing a comprehensive explanation suitable for both beginners and those seeking a deeper understanding. We'll explore different methods, highlight practical applications, and discuss the broader significance of LCM in mathematical contexts.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's solidify our understanding of the LCM. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the numbers in your set as factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Key Characteristics of LCM:
- Smallest Multiple: The LCM is always the smallest possible multiple that satisfies the divisibility condition.
- Divisibility: Every number in the set used to calculate the LCM must divide evenly into the resulting LCM.
- Applications: LCM finds extensive use in various mathematical operations, including simplifying fractions, solving problems involving time intervals, and working with rhythmic patterns.
Methods for Calculating the LCM of 5, 3, and 6
Several methods can efficiently compute the LCM of 5, 3, and 6. Let's explore the most common ones:
1. Listing Multiples Method
This method involves listing the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By inspecting the lists, we see that the smallest common multiple among the three sets is 30. Therefore, the LCM(5, 3, 6) = 30.
This method is straightforward for smaller numbers, but it becomes less efficient when dealing with larger numbers.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations and multiply them together:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
LCM(5, 3, 6) = 2 x 3 x 5 = 30
This method is generally more efficient for larger numbers than listing multiples.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are closely related. We can use the GCD to find the LCM using the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula directly applies only to two numbers. To extend it to three or more numbers, we need to find the GCD iteratively.
First, let's find the GCD of 5 and 3. Since 5 and 3 are prime numbers and have no common factors other than 1, their GCD is 1.
Next, we find the GCD of the result (1) and 6. The GCD of 1 and 6 is 1.
Now, we can use a modified approach:
- Find the LCM of 5 and 3: LCM(5,3) = 5 x 3 = 15
- Find the LCM of 15 and 6: We can use prime factorization: 15 = 3 x 5 and 6 = 2 x 3. The LCM(15,6) = 2 x 3 x 5 = 30
Therefore, LCM(5, 3, 6) = 30
Applications of LCM
The concept of LCM extends beyond theoretical mathematics; it finds practical applications in numerous real-world scenarios:
1. Scheduling and Time Management
Imagine you have three tasks that repeat at different intervals: Task A every 5 days, Task B every 3 days, and Task C every 6 days. To find when all three tasks will coincide, you need to calculate the LCM of 5, 3, and 6. The LCM, 30, indicates that all three tasks will align every 30 days.
2. Fraction Simplification
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the least common denominator, simplifying the fraction addition or subtraction process.
3. Music and Rhythmic Patterns
In music theory, LCM plays a role in understanding rhythmic patterns and finding the least common period where different rhythms synchronize.
4. Gear Ratios and Mechanical Engineering
In mechanical systems involving gears, the LCM helps determine the least common rotational period where gears with different numbers of teeth will align.
5. Cyclic Processes in Science
Many cyclical processes in science, such as the periodic recurrence of astronomical events, can be analyzed using LCM to predict their simultaneous occurrence.
Conclusion
Calculating the LCM of 5, 3, and 6, whether using the listing multiples, prime factorization, or GCD method, consistently yields the result of 30. This seemingly simple calculation underscores the fundamental importance of LCM in mathematics and its wide-ranging applications across various disciplines. Mastering the LCM concept empowers you to solve a plethora of problems related to time management, fractions, rhythmic patterns, and more. Understanding the different methods for calculating the LCM equips you to choose the most efficient approach depending on the complexity of the numbers involved. This comprehensive guide has equipped you with the knowledge and tools to confidently tackle LCM problems in diverse mathematical and real-world scenarios. Remember that consistent practice solidifies your understanding and enhances your problem-solving capabilities.
Latest Posts
Latest Posts
-
Where In A Plant Cell Does Photosynthesis Occur
Apr 02, 2025
-
A Motor And A Generator Are
Apr 02, 2025
-
Allows Materials In And Out Of The Cell
Apr 02, 2025
-
Which Of The Following Is Matched Correctly
Apr 02, 2025
-
Transitional Tissue Is Found In What System
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
