A Change In Velocity Is Known As
Juapaving
Apr 03, 2025 · 6 min read
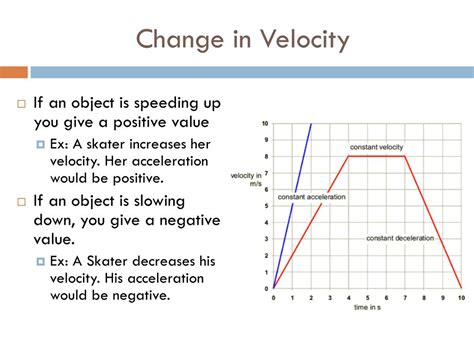
Table of Contents
A Change in Velocity is Known As: Acceleration Explained
A change in velocity is known as acceleration. This seemingly simple statement belies a concept that's fundamental to physics and crucial for understanding motion in all its forms, from the falling apple to the orbiting planets. While often associated with speeding up, acceleration encompasses more than just increasing speed. It's a vector quantity, meaning it has both magnitude (size) and direction. This article will delve deep into the concept of acceleration, exploring its definition, types, calculation, and real-world applications.
Understanding Velocity
Before we fully grasp acceleration, it's vital to understand velocity. Velocity is a vector quantity that describes the rate of change of an object's position with respect to time. It tells us not only how fast an object is moving (its speed), but also the direction of its motion. For example, a car traveling at 60 mph north has a different velocity than a car traveling at 60 mph south, even though their speeds are identical. Velocity is typically measured in meters per second (m/s) or kilometers per hour (km/h).
Defining Acceleration
Now, let's return to our core topic: acceleration. Acceleration is the rate of change of velocity with respect to time. This means that acceleration occurs whenever there's a change in either the speed or the direction of an object's motion, or both. It's important to emphasize the "rate of change" aspect – a constant velocity means zero acceleration. Acceleration is also a vector quantity; it has both magnitude (how much the velocity changes) and direction (the direction of the change in velocity).
Types of Acceleration
There are several ways to experience acceleration:
-
Positive Acceleration: This occurs when an object's velocity increases. Imagine a car speeding up from a stoplight; its velocity is increasing, resulting in positive acceleration.
-
Negative Acceleration (Deceleration): This occurs when an object's velocity decreases. A car slowing down to a stop exhibits negative acceleration, often referred to as deceleration or retardation. It's crucial to understand that negative acceleration doesn't necessarily mean the object is slowing down in the negative direction; it simply indicates a decrease in velocity.
-
Uniform Acceleration: This occurs when the velocity changes by the same amount in each unit of time. A ball falling freely under the influence of gravity near the Earth's surface experiences uniform acceleration (approximately 9.8 m/s² downwards).
-
Non-uniform Acceleration: This occurs when the velocity changes by varying amounts over time. A car accelerating from rest, then gradually slowing down, exhibits non-uniform acceleration.
-
Centripetal Acceleration: This is the acceleration experienced by an object moving in a circular path at a constant speed. Although the speed remains constant, the direction of motion is continuously changing, resulting in acceleration directed towards the center of the circle. This is crucial for understanding orbital mechanics and the motion of objects in rotating systems.
Calculating Acceleration
The acceleration (a) of an object can be calculated using the following formula:
a = (v<sub>f</sub> - v<sub>i</sub>) / t
Where:
- a represents acceleration
- v<sub>f</sub> represents the final velocity
- v<sub>i</sub> represents the initial velocity
- t represents the time taken for the change in velocity
This formula provides the average acceleration over a given time interval. For situations with non-uniform acceleration, more advanced calculus techniques are required to determine the instantaneous acceleration at any given point in time.
Units of Acceleration: The standard unit of acceleration is meters per second squared (m/s²), which signifies the change in velocity (m/s) per unit of time (s). Other units include kilometers per hour squared (km/h²) or feet per second squared (ft/s²).
Real-World Applications of Acceleration
Understanding acceleration is critical across numerous scientific and engineering disciplines. Here are a few examples:
-
Automotive Engineering: Designing and testing vehicles requires a deep understanding of acceleration. Engineers carefully calculate the acceleration curves to optimize performance, safety, and fuel efficiency. Anti-lock braking systems (ABS) are a prime example – they control wheel slip by modulating braking force and carefully managing acceleration/deceleration.
-
Aerospace Engineering: Rocket launches, airplane takeoffs, and orbital maneuvers all heavily rely on precise acceleration control. The forces involved are immense, and engineers must design systems that can withstand these forces while ensuring the safety of passengers and crew. Understanding both linear and angular acceleration is paramount.
-
Sports Science: Analyzing athletes' performance often involves studying their acceleration patterns. Coaches use this information to improve training strategies and enhance athletic performance. Understanding acceleration during sprints, jumps, and other athletic movements can significantly improve technique and results.
-
Physics and Astronomy: Newton's second law of motion (F = ma) directly links force, mass, and acceleration. This equation is fundamental to understanding motion and interactions between objects in classical mechanics. In astronomy, acceleration plays a vital role in understanding the gravitational interactions between celestial bodies, influencing their orbits and trajectories.
-
Robotics: In the field of robotics, precise control of acceleration is essential for smooth and controlled movements. Robots require sophisticated algorithms to navigate complex environments while avoiding collisions and performing tasks efficiently. The ability to precisely control the acceleration of robotic arms and mobile robots is fundamental to their functionality.
-
Medical Applications: Medical imaging techniques, such as MRI and CT scans, use the concept of acceleration to generate images. The acceleration and deceleration of particles within the body affect the resulting signal, which is then processed to create detailed images of internal organs and tissues.
Beyond the Basics: Advanced Concepts of Acceleration
The basic definition and calculation of acceleration provide a strong foundation, but several advanced concepts extend our understanding of this crucial concept:
-
Jerk: Jerk refers to the rate of change of acceleration. It essentially measures how quickly acceleration changes. A smooth ride in a car is characterized by low jerk, while abrupt changes in acceleration (e.g., sudden braking) lead to high jerk, which can be uncomfortable or even dangerous.
-
Angular Acceleration: While the previous discussion focuses on linear acceleration (changes in linear velocity), angular acceleration describes the rate of change of angular velocity (rotational speed). It's crucial for understanding rotational motion, important in many engineering applications, including rotating machinery and gyroscopic systems.
-
Relativistic Acceleration: In Einstein's theory of special relativity, the concept of acceleration becomes more complex. As an object's speed approaches the speed of light, its mass increases, and the relationship between force and acceleration changes. This necessitates a relativistic approach to analyzing acceleration at high speeds.
-
Acceleration in Multiple Dimensions: The simple formula we presented earlier works well for motion in one dimension (e.g., a car moving along a straight road). However, for motion in two or three dimensions (e.g., a projectile moving through the air), vectors and vector calculus must be used to accurately analyze the acceleration vector. This requires more sophisticated mathematical techniques to solve.
Conclusion: The Importance of Understanding Acceleration
Acceleration, despite its seemingly straightforward definition, is a powerful concept that underpins our understanding of motion in the universe. From the smallest particles to the largest galaxies, the laws of motion, particularly those governed by acceleration, determine how objects move and interact. A thorough grasp of acceleration, its different forms, its calculation, and its applications is crucial across numerous fields, enabling advancements in technology, engineering, and scientific understanding. This article provides a comprehensive overview, but further exploration of the topics mentioned—especially advanced calculus, vector calculus, and relativistic mechanics—will provide an even deeper understanding of this fundamental concept. By understanding acceleration, we unlock a deeper understanding of the physical world around us.
Latest Posts
Latest Posts
-
Evaluate The Trigonometric Function At The Quadrantal Angle
Apr 04, 2025
-
How Many Kilometers Is 11 Miles
Apr 04, 2025
-
170 Inches Is How Many Feet
Apr 04, 2025
-
Where In A Eukaryotic Cell Does Transcription Occur
Apr 04, 2025
-
Distance Covered Per Unit Of Time Is Called
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about A Change In Velocity Is Known As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
