98 As A Product Of Prime Factors
Juapaving
Mar 25, 2025 · 6 min read
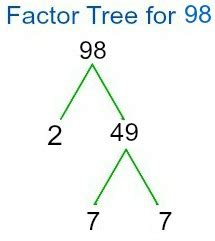
Table of Contents
98 as a Product of Prime Factors: A Deep Dive into Prime Factorization
Prime factorization, the process of breaking down a number into its prime number constituents, is a fundamental concept in number theory. Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM). This article delves into the prime factorization of 98, illustrating the process and exploring related concepts. We'll also look at how this seemingly simple example can help us grasp more complex ideas in number theory.
Understanding Prime Numbers and Prime Factorization
Before we embark on the factorization of 98, let's define key terms:
-
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. 2 is the only even prime number.
-
Composite Number: A composite number is a positive integer that has at least one divisor other than 1 and itself. All composite numbers can be expressed as a product of prime numbers.
-
Prime Factorization: This is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number (excluding the order of the factors).
Finding the Prime Factors of 98
Now, let's find the prime factorization of 98. We can use a factor tree or repeated division to achieve this.
Method 1: Factor Tree
-
Start with the number 98. We look for the smallest prime number that divides 98 evenly. This is 2.
-
Divide 98 by 2: 98 / 2 = 49.
-
Now we have 2 and 49. 2 is a prime number, but 49 is not.
-
Find the smallest prime factor of 49: This is 7.
-
Divide 49 by 7: 49 / 7 = 7.
-
We now have 2, 7, and 7. Both 2 and 7 are prime numbers.
Therefore, the prime factorization of 98 is 2 x 7 x 7, or 2 x 7<sup>2</sup>.
Method 2: Repeated Division
This method involves repeatedly dividing the number by its smallest prime factor until the quotient becomes 1.
-
Start with 98. The smallest prime factor is 2.
-
Divide 98 by 2: 98 / 2 = 49.
-
The next smallest prime factor of 49 is 7.
-
Divide 49 by 7: 49 / 7 = 7.
-
Finally, divide 7 by 7: 7 / 7 = 1.
The process stops when we reach 1. The prime factors are the numbers we used to divide: 2, 7, and 7. Again, the prime factorization is 2 x 7<sup>2</sup>.
Applications of Prime Factorization: Beyond 98
The seemingly simple factorization of 98 provides a foundation for understanding more complex mathematical concepts. Let's explore some applications:
1. Greatest Common Divisor (GCD)
The GCD of two or more numbers is the largest number that divides all of them without leaving a remainder. Prime factorization simplifies finding the GCD. For example, let's find the GCD of 98 and 140:
- Prime factorization of 98: 2 x 7<sup>2</sup>
- Prime factorization of 140: 2<sup>2</sup> x 5 x 7
To find the GCD, we identify the common prime factors and their lowest powers: Both numbers share a 2 and a 7. The lowest power of 2 is 2<sup>1</sup>, and the lowest power of 7 is 7<sup>1</sup>. Therefore, the GCD(98, 140) = 2 x 7 = 14.
2. Least Common Multiple (LCM)
The LCM of two or more numbers is the smallest number that is a multiple of all of them. Prime factorization simplifies finding the LCM. Let's find the LCM of 98 and 140:
- Prime factorization of 98: 2 x 7<sup>2</sup>
- Prime factorization of 140: 2<sup>2</sup> x 5 x 7
To find the LCM, we take the highest powers of all prime factors present in either number: The highest power of 2 is 2<sup>2</sup>, the highest power of 5 is 5<sup>1</sup>, and the highest power of 7 is 7<sup>2</sup>. Therefore, the LCM(98, 140) = 2<sup>2</sup> x 5 x 7<sup>2</sup> = 4 x 5 x 49 = 980.
3. Simplifying Fractions
Prime factorization is essential for simplifying fractions to their lowest terms. Consider the fraction 98/140:
- Prime factorization of 98: 2 x 7<sup>2</sup>
- Prime factorization of 140: 2<sup>2</sup> x 5 x 7
We can cancel out the common factors (2 and 7):
98/140 = (2 x 7 x 7) / (2 x 2 x 5 x 7) = 7/10
Therefore, the simplified fraction is 7/10.
4. Cryptography
Prime factorization plays a critical role in modern cryptography, particularly in RSA encryption. RSA relies on the difficulty of factoring large composite numbers into their prime factors. The security of many online transactions depends on the computational infeasibility of factoring extremely large numbers. While factoring 98 is trivial, the same principles apply to much larger numbers, making RSA encryption secure.
Exploring Further: Beyond the Basics
The prime factorization of 98, while seemingly simple, opens doors to deeper explorations within number theory:
-
Distribution of Prime Numbers: The prime factorization of numbers helps us study the distribution of prime numbers. While there's no simple formula to predict prime numbers, studying their occurrences within factorizations reveals patterns and contributes to ongoing research in number theory.
-
Modular Arithmetic: Understanding prime factors is crucial for working with modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). Modular arithmetic has extensive applications in cryptography and computer science.
-
Unique Factorization Theorem (Fundamental Theorem of Arithmetic): This theorem states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors). The prime factorization of 98 perfectly illustrates this fundamental theorem.
Conclusion: The Significance of a Simple Factorization
The prime factorization of 98, while a seemingly elementary mathematical operation, underscores the importance of prime numbers and prime factorization in number theory and its applications. From simplifying fractions to securing online transactions, the ability to decompose a number into its prime factors is a cornerstone of various mathematical and computational processes. By understanding this simple example, we can appreciate the power and elegance of prime factorization and its significant role in the broader world of mathematics and computer science. This foundational knowledge provides a stepping stone to exploring more advanced concepts in number theory and its diverse applications.
Latest Posts
Latest Posts
-
Nouns That Start With A V
Mar 28, 2025
-
A Piece Of Land Completely Surrounded By Water
Mar 28, 2025
-
What Is A Group Of Angels
Mar 28, 2025
-
What Is The Cubed Root Of 27
Mar 28, 2025
-
How Many Sig Figs In 0 04
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about 98 As A Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
