9 Is What Percent Of 4
Juapaving
May 12, 2025 · 5 min read
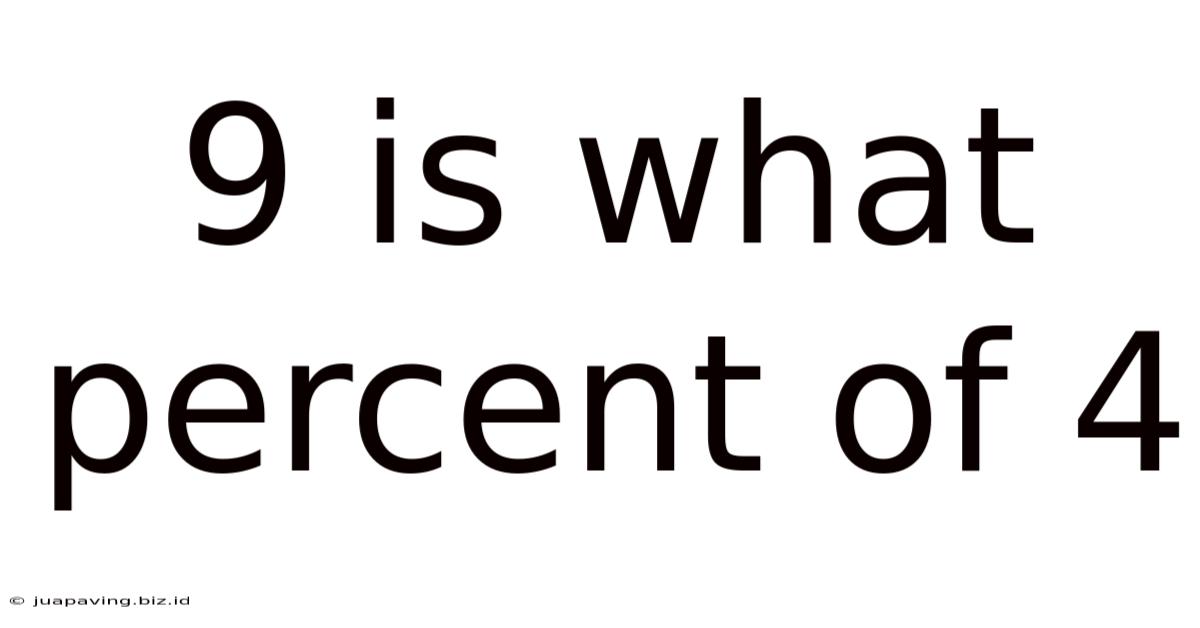
Table of Contents
9 is What Percent of 4? Unpacking the Math and its Applications
This seemingly simple question, "9 is what percent of 4?", opens the door to a fundamental concept in mathematics: percentages. While the calculation itself is straightforward, understanding the underlying principles and various applications expands its significance far beyond a simple arithmetic problem. This article will delve into the solution, explore the theoretical framework of percentages, and examine practical applications in diverse fields.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be converted into a decimal or a fraction. For instance, 50% is equivalent to 0.5 or 1/2, while 25% is 0.25 or 1/4. This interchangeability is crucial for solving percentage problems.
Calculating "9 is What Percent of 4?"
The question "9 is what percent of 4?" asks us to determine what percentage 9 represents when compared to 4. To solve this, we can follow these steps:
-
Set up the equation: We can represent the problem as an equation: x% of 4 = 9. Here, 'x' represents the unknown percentage we need to find.
-
Convert the percentage to a decimal: x% can be written as x/100.
-
Rewrite the equation: Substituting, we get (x/100) * 4 = 9.
-
Solve for x:
- Multiply both sides by 100: 4x = 900
- Divide both sides by 4: x = 225
Therefore, 9 is 225% of 4.
Interpreting the Result: More Than 100%
The result, 225%, might seem counterintuitive at first glance. It's important to remember that percentages can exceed 100%. This simply means that the first number (9) is larger than the second number (4). A percentage greater than 100% indicates a proportional increase, signifying that 9 is more than the whole of 4. This is perfectly valid within the mathematical framework of percentages.
Alternative Methods of Calculation
While the above method is systematic and readily understandable, alternative approaches can be used to solve this type of problem:
-
Using proportions: We can set up a proportion: 9/4 = x/100. Cross-multiplying and solving for x yields the same result: x = 225.
-
Direct calculation: We can directly calculate the ratio of 9 to 4 (9/4 = 2.25) and then multiply by 100% to obtain the percentage (2.25 * 100% = 225%). This method highlights the core relationship between fractions, decimals, and percentages.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial across many disciplines. Here are some examples:
-
Finance: Calculating interest rates, returns on investment, profit margins, discounts, and tax rates all rely heavily on percentage calculations. For example, determining the interest accrued on a loan or the percentage increase in a stock's value requires understanding percentage changes.
-
Business: Analyzing sales data, market share, growth rates, and cost-benefit analyses all depend on percentage calculations. For instance, tracking sales growth year-over-year or comparing market shares of competing companies requires precise percentage computations.
-
Science: Expressing experimental results, analyzing data sets, and calculating error margins often involve percentages. For example, scientific experiments might report their results as percentage increases or decreases relative to a control group.
-
Healthcare: Calculating dosages of medication, analyzing disease prevalence, and tracking treatment efficacy frequently use percentages. For example, determining the effectiveness of a treatment might involve calculating the percentage of patients who experienced improvement.
-
Everyday Life: Calculating tips at restaurants, understanding sales discounts, and interpreting statistical data in news reports all involve working with percentages. For instance, comprehending interest rates on credit cards or the percentage increase in inflation rates requires an understanding of percentage calculations.
Beyond Simple Calculations: Understanding Percentage Change
The problem "9 is what percent of 4?" focuses on a static comparison. However, often we are interested in percentage change. Percentage change measures the relative change between an initial and a final value. The formula is:
[(Final Value - Initial Value) / Initial Value] * 100%
For example, if the initial value is 4 and the final value is 9, the percentage change is:
[(9 - 4) / 4] * 100% = 125%
This indicates a 125% increase from the initial value to the final value. Understanding percentage change is essential for tracking trends, analyzing growth, and making informed decisions in various contexts.
Advanced Applications: Compound Interest and Exponential Growth
Percentage calculations play a fundamental role in understanding compound interest and exponential growth. Compound interest, often found in savings accounts and loans, involves earning interest not only on the principal but also on accumulated interest. The power of compounding is directly linked to percentage calculations, demonstrating how small percentage increases can lead to substantial growth over time.
Similarly, exponential growth, seen in phenomena like population growth or the spread of information, relies on percentage increase rates. These models use percentage growth rates to project future values based on present conditions. Understanding these applications requires a deeper understanding of percentage calculations and their role in mathematical modeling.
Addressing Common Mistakes and Misunderstandings
While percentage calculations are fundamental, some common mistakes can lead to inaccurate results:
-
Incorrect order of operations: It's crucial to follow the order of operations (PEMDAS/BODMAS) accurately when solving percentage problems involving multiple operations.
-
Confusing percentage increase with the final value: It's important to distinguish between the percentage increase and the final value after the increase.
-
Incorrect rounding: Rounding off numbers prematurely can lead to significant errors in the final result, especially when dealing with large numbers or multiple percentage calculations.
-
Failing to convert percentages to decimals or fractions: Forgetting to convert percentages to their decimal or fractional equivalents before performing calculations is a frequent source of errors.
Conclusion: The Ubiquity of Percentages
In conclusion, the seemingly simple question, "9 is what percent of 4?", provides a starting point for exploring the vast and versatile world of percentages. Understanding percentages is not merely about solving mathematical problems; it's about comprehending fundamental concepts applicable across countless fields. From finance and business to science and everyday life, the ability to accurately calculate and interpret percentages is a valuable skill that empowers informed decision-making and critical analysis. Mastering the principles and applications of percentages opens doors to a deeper understanding of numerical relationships and their significance in the world around us. By understanding the nuances of percentage calculations, including percentage change, compound interest, and exponential growth, you equip yourself with a powerful tool for navigating the complexities of quantitative information.
Latest Posts
Latest Posts
-
For The Following Distribution Find The Modal Class
May 12, 2025
-
List The First 5 Multiples Of 6
May 12, 2025
-
How Energy Is Lost In A Food Chain
May 12, 2025
-
What Fraction Of An Hour Is 45 Minutes
May 12, 2025
-
A Metal Crystallizes In A Face Centered Cubic Lattice
May 12, 2025
Related Post
Thank you for visiting our website which covers about 9 Is What Percent Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.