6 Is What Percent Of 45
Juapaving
May 12, 2025 · 4 min read
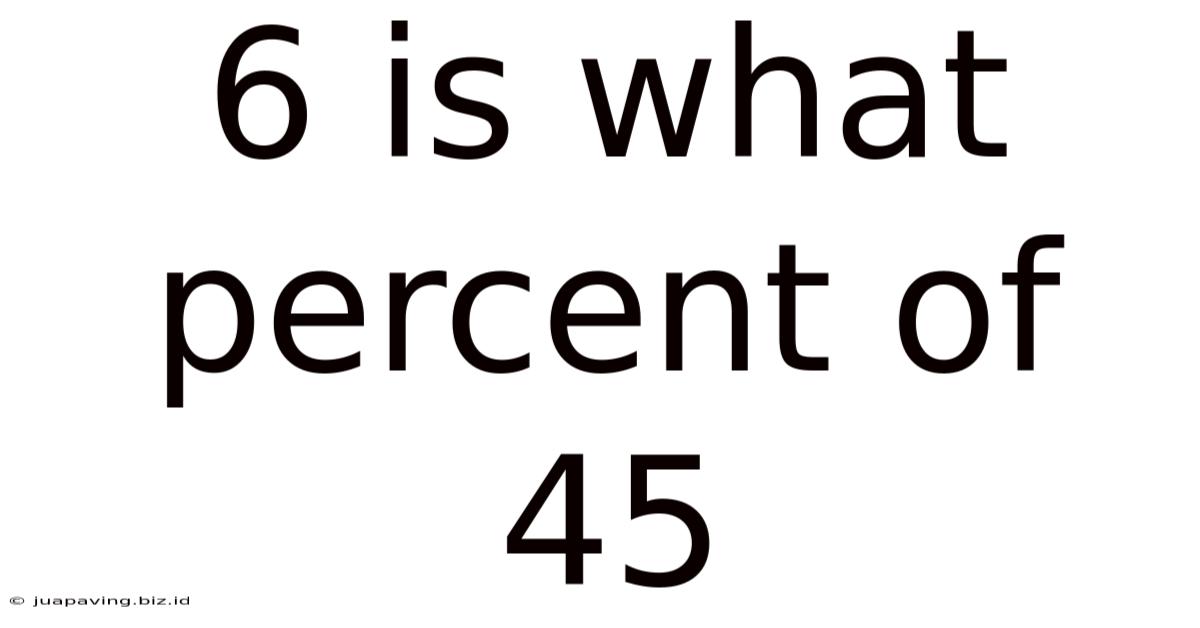
Table of Contents
6 is What Percent of 45: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to analyzing data and understanding statistical information. This article delves deep into the question, "6 is what percent of 45?", providing not only the answer but a comprehensive explanation of the underlying concepts and methods involved in solving percentage problems. We'll explore different approaches, practical applications, and helpful tips to enhance your understanding and calculation skills.
Understanding Percentages: The Basics
A percentage is simply a fraction or ratio expressed as a number out of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." When we say "x percent," we are essentially saying "x out of 100" or x/100. Therefore, understanding percentages fundamentally involves working with fractions and proportions.
Method 1: Using the Formula
The most straightforward method to determine what percent 6 is of 45 involves using a simple formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 6
- Whole: 45
Plugging these values into the formula:
(6 / 45) * 100% = 13.33% (approximately)
Therefore, 6 is approximately 13.33% of 45.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
6/45 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
6 * 100 = 45 * x
600 = 45x
x = 600 / 45
x = 13.33% (approximately)
This method confirms our previous result: 6 is approximately 13.33% of 45.
Method 3: Using Decimal Conversion
We can also solve this problem by first converting the fraction 6/45 into a decimal and then multiplying by 100% to express it as a percentage.
6 divided by 45 equals 0.1333...
Multiplying 0.1333... by 100% gives us 13.33%.
This method reinforces the equivalence between fractions, decimals, and percentages.
Practical Applications: Real-World Examples
The ability to calculate percentages is crucial in various real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offers a discount of $6 on an item originally priced at $45. Using the percentage calculation, we determine that the discount represents a 13.33% reduction. This allows customers to easily compare discounts from different stores.
2. Grade Calculations:
If a student scores 6 points out of a possible 45 points on a test, their score is 13.33%. This helps in assessing their performance relative to the total marks.
3. Financial Analysis:
In finance, percentages are used extensively. For instance, if a company's profit is $6 million out of a total revenue of $45 million, the profit margin is 13.33%. This is a key metric used to assess a company's financial health.
4. Data Analysis and Statistics:
Percentages are essential in data analysis and statistics. For example, if 6 out of 45 survey respondents answered "yes" to a question, the percentage of "yes" responses is 13.33%. This helps in summarizing and interpreting data.
Beyond the Basics: Working with More Complex Percentage Problems
While the problem "6 is what percent of 45?" is relatively straightforward, understanding the underlying principles enables you to tackle more complex percentage problems. Here are some common variations:
- Finding the whole: If you know the percentage and the part, you can calculate the whole. For example, "15% of what number is 9?"
- Finding the part: If you know the percentage and the whole, you can calculate the part. For example, "What is 20% of 80?"
- Percentage increase/decrease: These calculations involve finding the percentage change between two values. For example, "A value increased from 50 to 60. What is the percentage increase?"
- Compound percentages: These involve applying percentages multiple times. For example, "A value increases by 10% and then by another 5%. What is the total percentage increase?"
Tips for Mastering Percentage Calculations:
- Practice regularly: The key to mastering percentages is consistent practice. Solve various percentage problems to build your understanding and speed.
- Use a calculator: For more complex calculations, a calculator can be a valuable tool. Many calculators have a percentage function that simplifies the process.
- Understand the formula: Familiarize yourself with the basic percentage formula and how to adapt it to different scenarios.
- Break down complex problems: If you encounter a complex problem, break it down into smaller, more manageable steps.
- Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: Mastering the Percentage Power
The question, "6 is what percent of 45?", serves as a springboard to understanding the broader world of percentage calculations. By mastering the fundamental concepts and methods outlined in this article, you will be well-equipped to handle various percentage-related problems across different fields, improving your analytical skills and problem-solving abilities. Remember that consistent practice and a thorough understanding of the underlying principles are key to successfully navigating the world of percentages. So, practice regularly, and soon you'll be confidently tackling even the most challenging percentage calculations!
Latest Posts
Latest Posts
-
How To Calculate Density From Relative Density
May 13, 2025
-
What Percentage Is 7 Out Of 25
May 13, 2025
-
Plants Make Their Own Food Called
May 13, 2025
-
How To Find Diagonal Of Square
May 13, 2025
-
How Many Terms Are In The Expression
May 13, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percent Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.