What Percentage Is 7 Out Of 25
Juapaving
May 13, 2025 · 5 min read
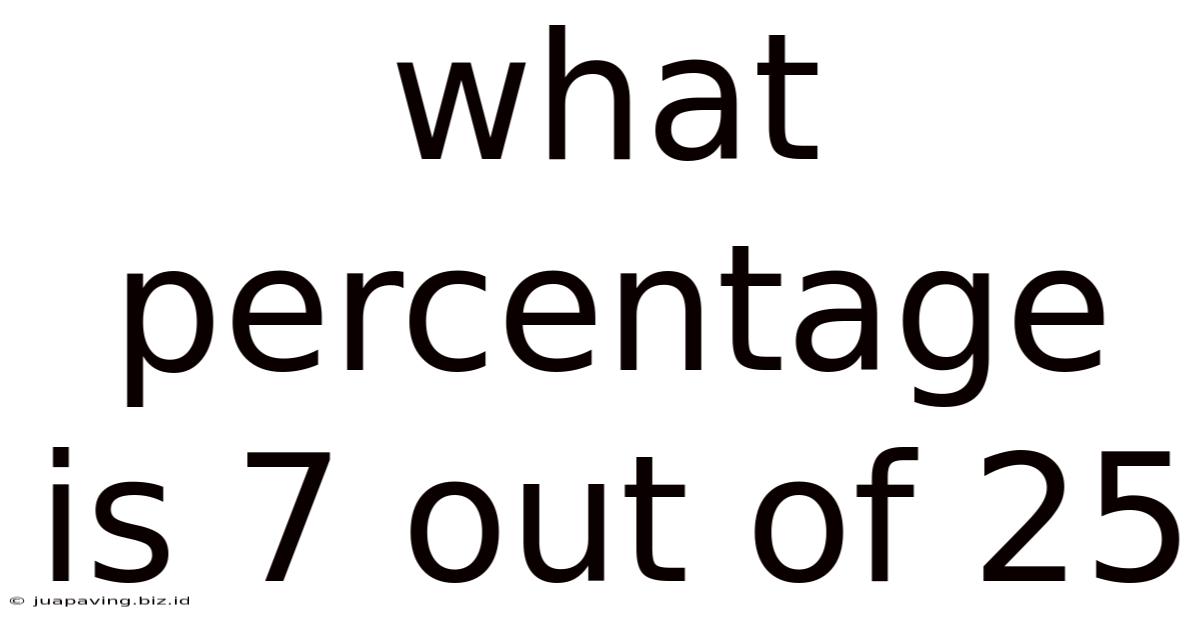
Table of Contents
What Percentage is 7 out of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into the question, "What percentage is 7 out of 25?", providing not only the answer but a comprehensive explanation of the underlying principles and various methods for solving similar percentage problems. We'll explore different calculation approaches, discuss practical applications, and even touch upon advanced percentage concepts.
Understanding the Basics of Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a portion of 100. The word "percent" literally means "out of 100" (per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding this fundamental concept is crucial for grasping percentage calculations. Every percentage problem involves three key components:
- The part: This is the number representing a portion of the whole. In our example, 7 is the part.
- The whole: This is the total number or the entire amount. In our example, 25 is the whole.
- The percentage: This is the fraction expressed as a portion of 100, representing the relationship between the part and the whole. This is what we need to calculate.
Calculating the Percentage: Method 1 - Using the Fraction Method
The most straightforward approach to calculating what percentage 7 out of 25 represents is to express the relationship as a fraction and then convert it to a percentage.
-
Form a fraction: Represent the problem as a fraction: 7/25.
-
Convert to a decimal: Divide the numerator (7) by the denominator (25): 7 ÷ 25 = 0.28
-
Convert to a percentage: Multiply the decimal by 100: 0.28 x 100 = 28%
Therefore, 7 out of 25 is 28%.
Calculating the Percentage: Method 2 - Using Proportions
Another effective method for solving percentage problems involves using proportions. This method is particularly useful for understanding the underlying relationship between the parts and the whole.
We set up a proportion:
Part/Whole = Percentage/100
Substituting our values:
7/25 = x/100
To solve for x (the percentage), we cross-multiply:
7 * 100 = 25 * x
700 = 25x
Now, divide both sides by 25:
x = 700 ÷ 25 = 28
Again, we find that 7 out of 25 is 28%.
Calculating the Percentage: Method 3 - Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function (%) that automates the process. Simply enter 7, divide by 25, and then multiply by 100 to get the result: 28%. The specific keystrokes may vary depending on your calculator model, but the fundamental steps remain the same. This is a fast and accurate method for everyday percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
-
Discounts: If a store offers a 20% discount on an item priced at $50, you can calculate the discount amount and the final price using percentage calculations.
-
Taxes: Calculating sales tax or income tax involves determining a percentage of a specific amount.
-
Grades: Many academic institutions express grades as percentages, representing the ratio of correctly answered questions to the total number of questions.
-
Statistics: Percentages are widely used in statistical analysis to present data in a concise and easily understandable format. For instance, analyzing survey results often involves expressing responses as percentages of the total respondents.
-
Finance: Interest rates, loan repayments, and investment returns are all expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Data Analysis: In data analysis, percentages are used to normalize data, allowing for easy comparison across different datasets. This is crucial in fields like business analytics, market research, and healthcare.
Advanced Percentage Concepts and Problem Solving
While the basic percentage calculation is straightforward, understanding more advanced concepts can significantly enhance your problem-solving skills.
-
Percentage Increase/Decrease: Calculating the percentage change between two values involves finding the difference between the values, dividing it by the original value, and then multiplying by 100.
-
Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest. This concept is fundamental in finance and investments.
-
Percentage Points: Percentage points represent the absolute difference between two percentages, not the relative difference. For example, an increase from 10% to 15% is a 5-percentage-point increase, not a 50% increase.
-
Solving for the Whole: In some problems, you might know the percentage and the part and need to calculate the whole. This involves setting up a proportion similar to the one used in Method 2 but solving for the "whole" instead of the percentage.
-
Multiple Percentages: Problems involving multiple percentages often require calculating the percentages sequentially. For example, applying a discount and then adding sales tax requires calculating each percentage separately in the correct order.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that can significantly improve your problem-solving abilities and enhance your understanding of numerical data in various contexts. Whether you're dealing with simple calculations or more complex percentage problems, understanding the underlying principles, using the right methods, and practicing regularly will build your confidence and proficiency in this crucial area of mathematics. Remember that practice makes perfect, so keep solving percentage problems to strengthen your skills and gain a deeper understanding of this fundamental mathematical concept. The ability to quickly and accurately calculate percentages is a valuable asset in both personal and professional life, empowering you to make better informed decisions and effectively analyze data in various situations. The simple example of calculating what percentage 7 out of 25 represents (28%) opens the door to a vast realm of applications where this skill is invaluable.
Latest Posts
Latest Posts
-
Polar Moment Of Inertia For Square
May 13, 2025
-
What Is The Basic Unit Of Nucleic Acid
May 13, 2025
-
How Do I Measure The Diameter Of A Ball
May 13, 2025
-
What Is Smaller Than A Cell
May 13, 2025
-
A Body Of Land Surrounded By Water
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 7 Out Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.