5 Postulates Of Kinetic Molecular Theory
Juapaving
Apr 02, 2025 · 6 min read
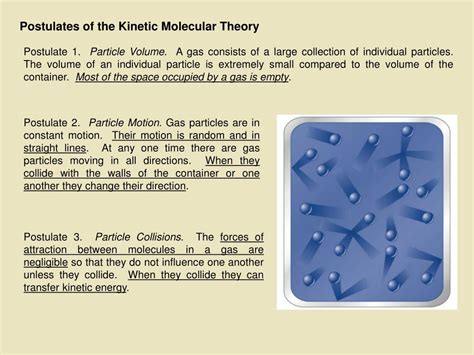
Table of Contents
5 Postulates of Kinetic Molecular Theory: A Deep Dive
The Kinetic Molecular Theory (KMT) is a fundamental model in chemistry that explains the macroscopic properties of gases based on the microscopic behavior of their constituent particles. Understanding these properties, such as pressure, temperature, and volume, is crucial in many scientific fields, from atmospheric science to chemical engineering. This theory rests on five key postulates, each contributing to a comprehensive understanding of gas behavior. Let's delve into each postulate in detail, exploring their implications and limitations.
Postulate 1: Gases are composed of tiny particles with negligible volume.
This first postulate establishes the fundamental building blocks of a gas: particles. These particles can be atoms or molecules, but crucially, their individual volumes are considered insignificant compared to the total volume occupied by the gas itself. Imagine a basketball filled with tiny marbles; the volume of the marbles themselves is negligible compared to the overall volume of the basketball. Similarly, the space between gas particles is vast, and the particles themselves contribute minimally to the overall volume.
This assumption simplifies calculations significantly. It allows us to treat gases as ideal gases, where particle volume is disregarded. While real gases deviate from this ideal behavior at high pressures (where particle volumes become significant relative to the total volume), the ideal gas approximation provides a valuable starting point for understanding many gas properties.
Implications:
- Ideal Gas Law: This postulate directly contributes to the derivation of the Ideal Gas Law (PV=nRT), a cornerstone equation in chemistry. The neglect of particle volume makes the equation more tractable and applicable to a wide range of gas behaviors at moderate pressures and temperatures.
- Compression: The negligible volume of gas particles means that gases are easily compressible. Applying pressure reduces the intermolecular spacing, decreasing the overall volume. This is starkly different from solids and liquids, where the particles are already tightly packed.
Limitations:
- High Pressure: At high pressures, the volume of the gas particles becomes significant enough to affect the overall volume of the gas, leading to deviations from ideal gas behavior. Real gas equations, such as the van der Waals equation, incorporate corrections to account for particle volume.
- Low Temperature: At extremely low temperatures, intermolecular forces become more dominant, influencing the behavior of the gas particles more significantly. Again, ideal gas law becomes less applicable in these conditions.
Postulate 2: Gas particles are in constant, random motion.
Unlike solids and liquids, where particles are relatively fixed in position, gas particles are in perpetual, chaotic motion. This constant movement is responsible for many of the observable properties of gases. This motion is random, meaning that the particles move in unpredictable directions and speeds.
This postulate explains phenomena like diffusion and effusion. Diffusion is the spreading of gases to occupy all available space, while effusion is the escape of gases through a tiny hole. Both processes rely on the incessant movement and random trajectories of the gas particles.
Implications:
- Pressure: The constant bombardment of gas particles against the walls of their container creates pressure. More frequent and forceful collisions result in higher pressure. This is directly related to the temperature and number of particles present.
- Diffusion and Effusion: The random motion of gas particles leads to their spontaneous mixing (diffusion) and their ability to escape from a container through a small opening (effusion). Grahams law of effusion is directly derived from this postulate.
Limitations:
- Absolute Zero: While theoretically the motion never stops entirely until absolute zero, practically at extremely low temperatures, the motion becomes significantly slower and intermolecular forces play a greater role.
Postulate 3: Collisions between gas particles and between gas particles and the container walls are elastic.
Elastic collisions mean that no energy is lost during the collision. When gas particles collide with each other or the container walls, the total kinetic energy of the system is conserved. This means that the particles may change direction and speed after a collision, but the overall kinetic energy remains constant.
This postulate simplifies the analysis of gas behavior, allowing us to focus on the transfer of momentum without needing to consider energy loss through friction or other dissipative forces.
Implications:
- Conservation of Energy: The elastic collision postulate ensures that the total kinetic energy of the gas is conserved, which is crucial for maintaining the equilibrium state of the system.
- Temperature: The average kinetic energy of the gas particles is directly proportional to the absolute temperature. As temperature increases, the particles move faster, resulting in more frequent and forceful collisions.
Limitations:
- Real Gases: Real gases exhibit some inelastic collisions due to intermolecular forces. These forces may lead to temporary attraction or repulsion between particles, resulting in slight energy loss. However, at moderate temperatures and pressures, this effect is often negligible.
Postulate 4: The average kinetic energy of gas particles is proportional to the absolute temperature.
This postulate directly links the macroscopic property of temperature to the microscopic property of kinetic energy. The absolute temperature (in Kelvin) is a direct measure of the average kinetic energy of the gas particles. Higher temperatures imply faster-moving particles with higher kinetic energy.
This postulate is crucial for understanding the relationship between temperature and other gas properties such as pressure and volume.
Implications:
- Temperature and Pressure: Increasing temperature increases the average kinetic energy, leading to more frequent and forceful collisions with the container walls, thereby increasing pressure.
- Temperature and Volume: At constant pressure, increasing temperature increases the volume, as the particles move faster and push against the container walls with greater force.
Limitations:
- Intermolecular Forces: At lower temperatures, intermolecular forces can significantly affect the average kinetic energy, causing deviations from the direct proportionality.
Postulate 5: The gas particles occupy a negligible volume compared to the volume of the container.
This postulate reiterates the first postulate, emphasizing the vastness of the space between gas particles relative to their own size. This means that the gas particles themselves do not significantly contribute to the overall volume of the gas.
This reinforces the ideal gas assumption and underlies many calculations involving gas properties.
Implications:
- Ideal Gas Law Applicability: This postulate further supports the applicability of the ideal gas law, which assumes negligible particle volume.
- Gas Expansibility: Gases readily expand to fill the available volume because of the large space between particles.
Limitations:
- High Pressure Scenarios: As mentioned previously, this assumption breaks down at high pressures where the volume of the gas particles becomes significant relative to the total volume.
Conclusion:
The five postulates of the Kinetic Molecular Theory provide a powerful framework for understanding the behavior of gases. While the theory makes several simplifying assumptions, which lead to limitations primarily at high pressures and low temperatures, it serves as an excellent model for a wide range of gas behaviors. Understanding these postulates is crucial for comprehending various chemical and physical phenomena involving gases, solidifying its importance as a cornerstone of chemistry. By appreciating both the strengths and limitations of KMT, we can more effectively predict and explain the macroscopic behavior of gases based on their microscopic properties. Further exploration of real gas behavior and deviations from ideality helps to build a more nuanced and comprehensive understanding of gas dynamics.
Latest Posts
Latest Posts
-
A Nucleotide Is Made Of Three Parts
Apr 03, 2025
-
Who Is The Father Of Sociology
Apr 03, 2025
-
Whats The Square Root Of 30
Apr 03, 2025
-
How Many Feet Is 18 Yards
Apr 03, 2025
-
Facts And Statistics Collected Together For Reference Or Analysis
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 5 Postulates Of Kinetic Molecular Theory . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
