44 As A Product Of Prime Factors
Juapaving
Mar 28, 2025 · 5 min read
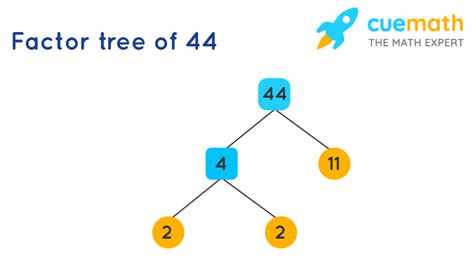
Table of Contents
- 44 As A Product Of Prime Factors
- Table of Contents
- 44 as a Product of Prime Factors: A Deep Dive into Prime Factorization
- Understanding Prime Numbers and Prime Factorization
- What are Prime Numbers?
- What is Prime Factorization?
- Factorizing 44: A Step-by-Step Approach
- The Uniqueness of the Prime Factorization of 44
- Applications of Prime Factorization
- 1. Cryptography
- 2. Modular Arithmetic
- 3. Number Theory
- 4. Computer Science
- Beyond 44: Exploring Other Prime Factorizations
- Conclusion: The Enduring Importance of Prime Factorization
- Latest Posts
- Latest Posts
- Related Post
44 as a Product of Prime Factors: A Deep Dive into Prime Factorization
Prime factorization, a cornerstone of number theory, is the process of expressing a composite number as a product of its prime factors. Understanding this process unlocks deeper insights into number properties and has practical applications in various mathematical fields, including cryptography and modular arithmetic. This article will delve into the prime factorization of 44, exploring the methods involved, demonstrating the uniqueness of the prime factorization, and discussing its broader significance within number theory.
Understanding Prime Numbers and Prime Factorization
Before we embark on factorizing 44, let's establish a firm understanding of the fundamental concepts.
What are Prime Numbers?
Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. This means they have exactly two distinct positive divisors. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The infinitude of prime numbers is a well-established theorem in number theory, meaning there are infinitely many prime numbers.
What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of expressing a composite number (a number greater than 1 that is not prime) as a unique product of its prime factors. This means representing the number as a multiplication of prime numbers only. For example, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3. The uniqueness of prime factorization is a crucial property; every composite number has only one prime factorization (ignoring the order of the factors). This is known as the Fundamental Theorem of Arithmetic.
Factorizing 44: A Step-by-Step Approach
Now, let's tackle the prime factorization of 44. There are several methods to achieve this, but the most common and straightforward is the method of successive division.
Method 1: Successive Division
-
Start with the smallest prime number, 2. Since 44 is an even number, it's divisible by 2. 44 ÷ 2 = 22.
-
Continue dividing by the smallest prime number. 22 is also an even number, divisible by 2. 22 ÷ 2 = 11.
-
Identify the prime factor. 11 is a prime number. We cannot divide it further by any prime number other than itself.
-
Write the prime factorization. Therefore, the prime factorization of 44 is 2 x 2 x 11, which can be written more concisely as 2² x 11.
Method 2: Factor Tree
Another way to visualize the prime factorization is using a factor tree.
44
/ \
2 22
/ \
2 11
The factor tree starts with the number 44. We branch it into its smallest prime factor (2) and the resulting quotient (22). We then continue this process for 22, branching it into 2 and 11. Since both 2 and 11 are prime numbers, we stop here. Reading the "leaves" of the tree (the bottom numbers), we get the prime factors: 2, 2, and 11. This confirms that the prime factorization of 44 is 2² x 11.
The Uniqueness of the Prime Factorization of 44
The Fundamental Theorem of Arithmetic guarantees that the prime factorization of 44 (2² x 11) is unique. No matter which method we use, we will always arrive at the same prime factors. This uniqueness is essential for many mathematical operations and theorems. For instance, the greatest common divisor (GCD) and the least common multiple (LCM) of two numbers can be efficiently calculated using their prime factorizations.
Applications of Prime Factorization
The concept of prime factorization is far from being a purely theoretical exercise. It has significant applications in various fields:
1. Cryptography
Modern cryptography heavily relies on prime numbers and their properties. RSA encryption, one of the most widely used public-key cryptosystems, utilizes the difficulty of factoring large numbers into their prime factors. The security of RSA depends on the infeasibility of factoring the product of two very large prime numbers in a reasonable amount of time.
2. Modular Arithmetic
Prime factorization plays a crucial role in modular arithmetic, a branch of number theory dealing with remainders after division. Concepts like Euler's totient function, which is used in cryptography, are directly related to prime factorization.
3. Number Theory
Prime factorization is fundamental to many number theory theorems and concepts. It provides a powerful tool for investigating the properties of integers and solving number theory problems. Understanding prime factorization is essential for grasping other advanced concepts like congruences, quadratic residues, and algebraic number theory.
4. Computer Science
Algorithms for finding prime factors are extensively studied in computer science. The efficiency of these algorithms impacts the performance of cryptographic systems and other applications. The development of faster factorization algorithms remains an active area of research.
Beyond 44: Exploring Other Prime Factorizations
While we've focused on 44, the principles of prime factorization apply to any composite number. Let's briefly explore a few more examples:
- 100: 100 = 2 x 2 x 5 x 5 = 2² x 5²
- 120: 120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
- 252: 252 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7
- 1024: 1024 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2¹⁰
Notice that each number has a unique prime factorization. This reinforces the Fundamental Theorem of Arithmetic, which is a cornerstone of number theory.
Conclusion: The Enduring Importance of Prime Factorization
The seemingly simple process of prime factorization has profound implications across various fields. Its importance stems from the fundamental theorem of arithmetic, guaranteeing the uniqueness of prime factorization for every composite number. This uniqueness is crucial for advanced mathematical concepts, cryptographic systems, and computational algorithms. Understanding prime factorization is not merely about breaking down numbers; it's about unlocking a deeper understanding of the structure and properties of the number system itself, contributing to significant advancements in mathematics and computer science. The seemingly simple example of 44's prime factorization (2² x 11) serves as a perfect gateway to appreciating the power and elegance of this core mathematical concept.
Latest Posts
Latest Posts
-
Where Does Sound Waves Travel Fastest
Apr 01, 2025
-
How Many Grams Is 5 Kg
Apr 01, 2025
-
Newtons First Law Examples In Everyday Life
Apr 01, 2025
-
15 4 As A Mixed Number
Apr 01, 2025
-
What Organelle Is The Site Of Aerobic Respiration
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 44 As A Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
