150 Is What Percent Of 200
Juapaving
May 12, 2025 · 5 min read
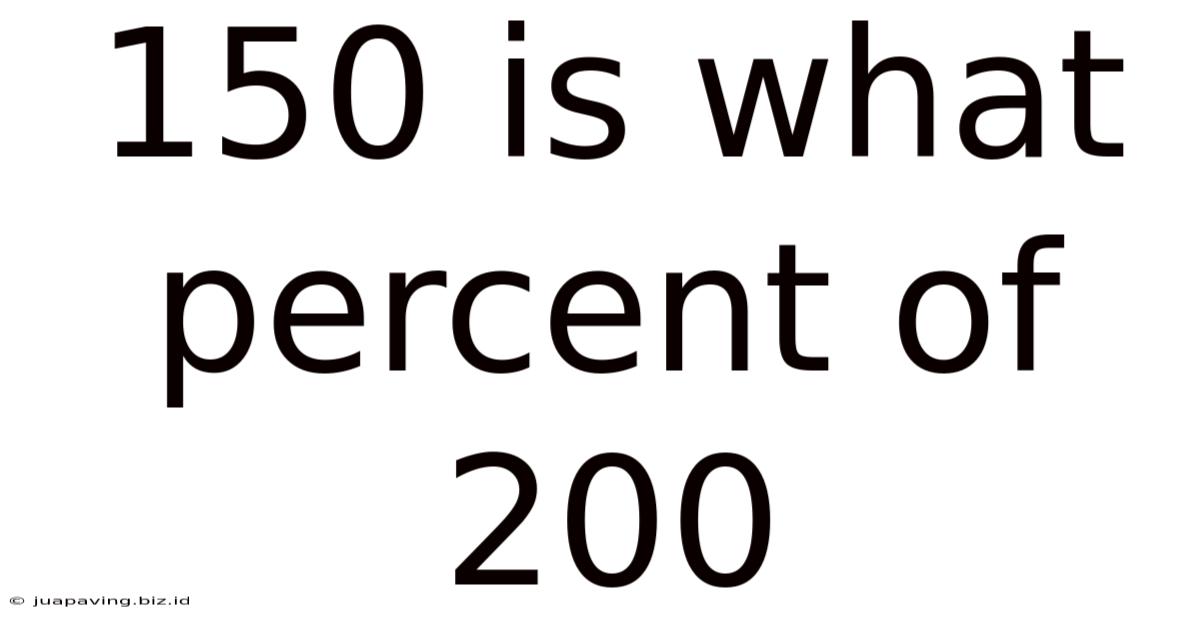
Table of Contents
150 is What Percent of 200: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to solve percentage problems efficiently and accurately is crucial for making informed decisions and navigating numerical data effectively. This comprehensive guide will delve into the intricacies of calculating percentages, focusing specifically on the question: "150 is what percent of 200?" We'll explore multiple methods, providing a step-by-step approach for easy comprehension, along with practical examples and real-world applications.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" denotes percentage. For example, 50% means 50 out of 100, which can also be written as the fraction 50/100 or the decimal 0.5.
Percentages are used extensively to represent proportions, ratios, and rates of change. They offer a standardized way to compare different quantities and make sense of data across various contexts.
Method 1: Using the Formula
The most straightforward way to determine what percentage 150 represents of 200 is using the basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 150
- Whole: 200
Substituting these values into the formula:
(150 / 200) * 100 = 75%
Therefore, 150 is 75% of 200.
Method 2: Cross-Multiplication
This method involves setting up a proportion and solving for the unknown percentage. We can represent the problem as:
150 / 200 = x / 100
Where 'x' represents the percentage we want to find.
To solve this proportion, we cross-multiply:
150 * 100 = 200 * x
15000 = 200x
Now, we solve for 'x' by dividing both sides by 200:
x = 15000 / 200
x = 75
Therefore, 150 is 75% of 200.
Method 3: Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
First, we express the relationship between 150 and 200 as a fraction:
150 / 200
Next, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (50):
150 / 200 = 3 / 4
Now, we convert the fraction 3/4 into a decimal by dividing the numerator by the denominator:
3 / 4 = 0.75
Finally, we multiply the decimal by 100 to express it as a percentage:
0.75 * 100 = 75%
Thus, 150 is 75% of 200.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is vital in a multitude of real-world scenarios. Here are some examples:
1. Sales and Discounts:
Retail stores frequently offer discounts expressed as percentages. For example, a "25% off" sale means you pay 75% of the original price. Calculating the final price after a discount requires understanding percentage calculations.
Example: A shirt originally costs $50 and is on sale for 20% off. The discount is 20% of $50, which is ($50 * 0.20) = $10. The final price is $50 - $10 = $40.
2. Taxes and Tips:
Sales tax and service tips are typically expressed as percentages. Knowing how to calculate these percentages accurately is crucial for managing personal finances.
Example: A meal costs $75, and the sales tax is 6%. The tax amount is ($75 * 0.06) = $4.50. The total cost including tax is $75 + $4.50 = $79.50. If you want to leave a 15% tip, that would be ($75 * 0.15) = $11.25.
3. Financial Analysis:
Percentage calculations are fundamental in financial analysis, used to calculate return on investment (ROI), profit margins, and growth rates.
Example: An investment of $1000 grows to $1200. The percentage increase is calculated as: (($1200 - $1000) / $1000) * 100 = 20%. This means a 20% return on investment.
4. Grade Calculations:
In academic settings, percentages are used to represent grades and scores. Calculating your overall grade often involves converting individual scores into percentages.
Example: If you scored 45 out of 50 on a test, your percentage score is (45/50) * 100 = 90%.
5. Data Analysis and Statistics:
Percentages are frequently used to represent data in graphs, charts, and statistical reports. Understanding percentages is essential for interpreting these visualizations and drawing meaningful conclusions.
Beyond the Basics: More Complex Percentage Problems
While the problem "150 is what percent of 200?" is relatively straightforward, percentage calculations can become more complex. These often involve multiple steps or require working backwards from a known percentage to find the original value.
For instance, you might encounter problems like:
- Finding the original value: If a discounted price is $60 after a 20% discount, what was the original price?
- Calculating percentage increase or decrease: What is the percentage increase from 50 to 75?
- Compound percentages: Calculating interest that accrues over multiple periods, where the interest is added to the principal each time.
Solving these more advanced percentage problems often involves applying the basic percentage formula in multiple steps or rearranging the formula to solve for different variables. Practice and familiarity with the core concepts will greatly enhance your ability to tackle these challenges effectively.
Conclusion
Calculating percentages is a skill that transcends academic settings and finds practical application in diverse aspects of everyday life. Understanding the various methods for calculating percentages, such as using the formula, cross-multiplication, and decimal conversion, equips you with the tools to solve a wide range of problems accurately and efficiently. Mastering percentage calculations improves financial literacy, strengthens analytical skills, and allows for a deeper understanding of numerical data presented in various formats. Consistent practice and application of these methods will solidify your understanding and make percentage calculations second nature. Remember, the fundamental principle remains the same across all these variations: relating a part to a whole and expressing that relationship as a fraction of 100.
Latest Posts
Latest Posts
-
Another Name For Newtons First Law
May 12, 2025
-
The Two Points That Define The Latus Rectum Are
May 12, 2025
-
5 Letter Word That Starts With Ad
May 12, 2025
-
1 To 50 Elements With Symbols
May 12, 2025
-
2 3 5 7 11 13 17
May 12, 2025
Related Post
Thank you for visiting our website which covers about 150 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.