2 3 5 7 11 13 17
Juapaving
May 12, 2025 · 6 min read
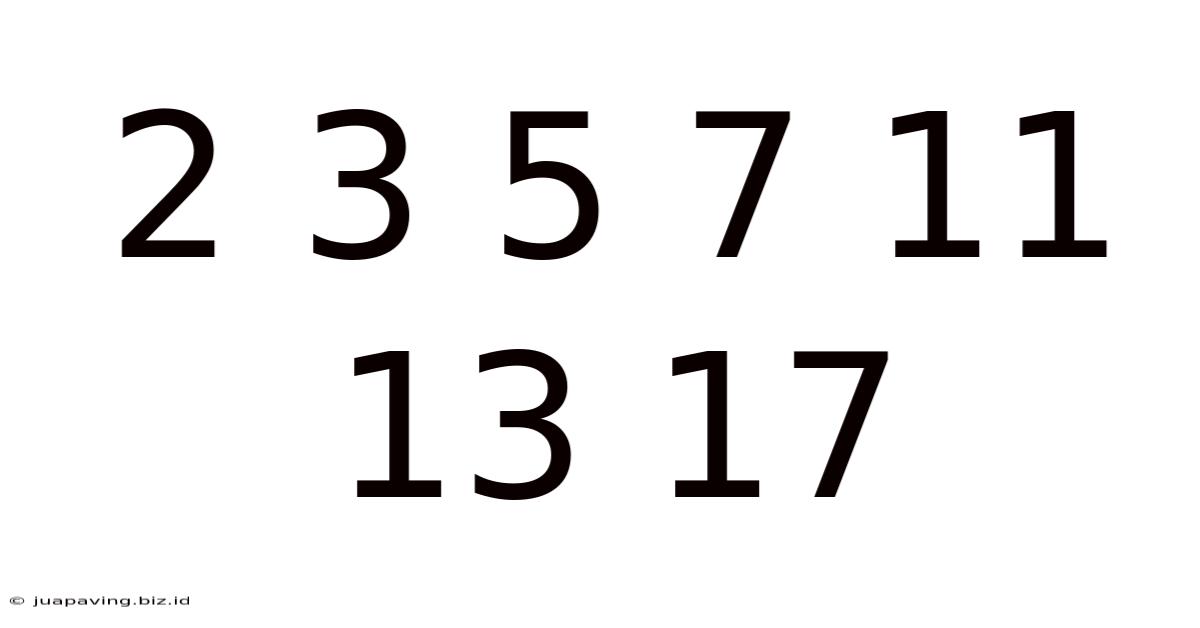
Table of Contents
Decoding the Sequence: 2, 3, 5, 7, 11, 13, 17... and the Allure of Prime Numbers
The seemingly simple sequence – 2, 3, 5, 7, 11, 13, 17 – holds a captivating power for mathematicians and number enthusiasts alike. At first glance, it might appear unremarkable, just a collection of numbers. However, a closer inspection reveals these aren't just any numbers; they are the first seven prime numbers. This seemingly simple sequence opens a door to a fascinating world of mathematical exploration, riddled with unsolved problems and profound implications. This article delves deep into the nature of prime numbers, their properties, their significance in cryptography, and the ongoing quest to understand their distribution.
Understanding Prime Numbers: The Building Blocks of Arithmetic
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly simple definition belies the profound complexity of prime numbers. They are the fundamental building blocks of all other integers, just as atoms are the fundamental building blocks of matter. Any whole number greater than 1 can be uniquely expressed as a product of prime numbers – a concept known as the Fundamental Theorem of Arithmetic.
For example:
- 12 = 2 x 2 x 3
- 35 = 5 x 7
- 100 = 2 x 2 x 5 x 5
This decomposition into prime factors is unique, meaning there's only one way to express a number as a product of primes (disregarding the order of the factors). This fundamental property underpins much of modern number theory and has far-reaching applications.
Identifying Prime Numbers: Methods and Challenges
Determining whether a large number is prime can be computationally intensive. While simple methods like trial division (checking divisibility by all numbers up to its square root) work for smaller numbers, they become inefficient for very large numbers. Sophisticated algorithms, like the Miller-Rabin primality test and the AKS primality test, are employed to determine the primality of large numbers used in cryptography. These probabilistic tests offer a high degree of certainty, but they don't provide absolute proof in the same way as deterministic tests.
The challenge of finding large prime numbers is intimately linked to the distribution of primes themselves, a topic that has captivated mathematicians for centuries.
The Distribution of Prime Numbers: A Pattern in Chaos?
The sequence 2, 3, 5, 7, 11, 13, 17... suggests an initial regularity. However, as we move to larger numbers, the spacing between primes becomes increasingly unpredictable. While the primes initially seem to appear with some frequency, the gaps between consecutive primes can become arbitrarily large. This irregularity is precisely what makes the study of prime number distribution so challenging and fascinating.
The Prime Number Theorem: An Asymptotic Approximation
Despite the irregularity, there is a pattern. The Prime Number Theorem provides an asymptotic approximation of the number of primes less than or equal to a given number. It states that the number of primes less than or equal to x is approximately x/ln(x), where ln(x) is the natural logarithm of x. This theorem doesn't provide an exact count, but it gives a remarkably accurate estimate for large values of x.
This means that although the distribution of primes is irregular, the overall density of primes tends to decrease as we move to larger numbers. However, even with this theorem, predicting the exact location of the next prime remains a significant challenge.
Gaps Between Primes: Twin Primes and Beyond
The gaps between consecutive prime numbers vary considerably. Some gaps are small, while others are extraordinarily large. Twin primes, pairs of primes that differ by 2 (like 3 and 5, or 11 and 13), are a particularly interesting area of research. The Twin Prime Conjecture posits that there are infinitely many twin prime pairs, but this remains an unsolved problem.
Other notable prime-related concepts include:
- Cousin primes: Pairs of primes differing by 4.
- Sexy primes: Pairs of primes differing by 6.
- Prime gaps: The difference between consecutive primes.
The study of prime gaps provides valuable insights into the erratic yet patterned behavior of prime numbers. The seemingly chaotic distribution hides underlying structures that are yet to be fully understood.
Prime Numbers in Cryptography: Securing the Digital World
The unique properties of prime numbers are crucial in modern cryptography. Many encryption algorithms rely on the difficulty of factoring large numbers into their prime components. The seemingly simple act of multiplying two large prime numbers is computationally easy, but the reverse process – factoring the product back into its prime factors – is incredibly difficult for sufficiently large numbers.
This computational asymmetry forms the basis of many public-key cryptosystems. Algorithms like RSA (Rivest-Shamir-Adleman) utilize this principle to secure online transactions, communications, and data storage. The security of these systems depends on the difficulty of factoring large semiprimes (numbers that are the product of two large prime numbers). As computing power increases, the size of the prime numbers used in cryptography must also increase to maintain security.
The Ongoing Quest for Larger Primes: A Race Against Time and Technology
The search for larger and larger prime numbers is an ongoing pursuit. Finding these primes is not just a theoretical exercise; it has practical implications for cryptography. Larger primes provide stronger security, safeguarding our digital world from potential breaches. The Great Internet Mersenne Prime Search (GIMPS) is a distributed computing project that continuously searches for Mersenne primes (primes of the form 2<sup>p</sup> - 1, where p is also a prime). The discovery of each new largest prime is a testament to the power of collaboration and computational advancements.
The Riemann Hypothesis: A Millennium Problem and its Link to Primes
One of the most significant unsolved problems in mathematics is the Riemann Hypothesis. This conjecture, proposed by Bernhard Riemann in 1859, relates to the distribution of prime numbers and the zeros of the Riemann zeta function. The Riemann zeta function is a complex function that encodes information about the distribution of prime numbers. The Riemann Hypothesis states that all non-trivial zeros of the Riemann zeta function lie on a specific line in the complex plane.
While seemingly abstract, the Riemann Hypothesis has profound implications for our understanding of the distribution of prime numbers. Its proof or disproof would have significant consequences for number theory and potentially other areas of mathematics and physics. The Clay Mathematics Institute has offered a US$1 million prize for a correct proof of the Riemann Hypothesis, highlighting its importance and difficulty.
Conclusion: The Enduring Mystery and Practical Importance of Prime Numbers
The sequence 2, 3, 5, 7, 11, 13, 17… opens a window into the enigmatic world of prime numbers. These numbers, the building blocks of arithmetic, exhibit a fascinating blend of regularity and unpredictability. Their distribution is a subject of ongoing research, with unsolved problems like the Twin Prime Conjecture and the Riemann Hypothesis fueling continued exploration. Beyond their theoretical significance, prime numbers play a vital role in securing our digital world, forming the bedrock of modern cryptography. The quest to understand prime numbers continues, driving advancements in both theoretical mathematics and practical applications, making them a truly remarkable and essential part of the mathematical landscape.
Latest Posts
Latest Posts
-
How Many Ounces Is A Bag Of Sugar
May 13, 2025
-
Label The Parts Of The Noncyclic Pathway
May 13, 2025
-
What Does Represent Mean In Math
May 13, 2025
-
Which Of The Following Statements About Viruses Is True
May 13, 2025
-
Is Iron An Element Or Compound
May 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 13 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.