1/8 Of A Circle Is What Percent
Juapaving
Apr 03, 2025 · 5 min read
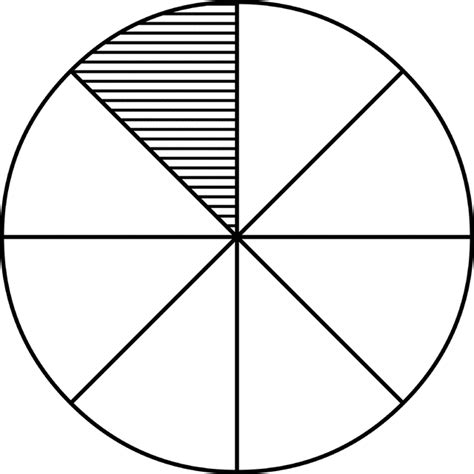
Table of Contents
1/8 of a Circle is What Percent? A Comprehensive Guide to Circle Fractions and Percentages
Understanding fractions and percentages of circles is crucial in various fields, from geometry and mathematics to design and data visualization. This comprehensive guide will delve into the intricacies of calculating the percentage represented by 1/8 of a circle, explaining the process step-by-step and providing practical examples. We'll also explore related concepts to solidify your understanding and equip you with the tools to tackle similar problems.
Understanding the Fundamentals: Circles, Fractions, and Percentages
Before diving into the specifics of 1/8 of a circle, let's review the core concepts:
Circles: A circle is a two-dimensional geometric shape defined as a set of points equidistant from a central point. Key characteristics include the radius (distance from the center to any point on the circle) and the diameter (twice the radius, passing through the center). The circumference is the distance around the circle.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, and the numerator indicates how many of those parts are being considered. For example, 1/8 means one part out of eight equal parts.
Percentages: A percentage is a way of expressing a fraction or a ratio as a portion of 100. The symbol "%" represents "per hundred". For instance, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
Calculating the Percentage: 1/8 of a Circle
To determine what percentage 1/8 represents of a whole circle, we need to convert the fraction into a percentage. Here's how:
-
Set up the Fraction: We start with the fraction 1/8. This represents one part out of eight equal parts of a circle.
-
Convert to Decimal: To convert a fraction to a percentage, we first convert it to a decimal by dividing the numerator by the denominator:
1 ÷ 8 = 0.125
-
Convert Decimal to Percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.125 × 100 = 12.5%
Therefore, 1/8 of a circle is 12.5%.
Visualizing 1/8 of a Circle
Imagine a pie cut into eight equal slices. Each slice represents 1/8 of the whole pie. If you take one slice, you have 12.5% of the entire pie. This visualization makes the concept more intuitive and easier to grasp.
Practical Applications and Real-World Examples
The concept of calculating fractions and percentages of circles has numerous applications across various disciplines:
-
Data Visualization: Pie charts are a common way to represent data proportionally. Each segment of a pie chart represents a fraction of the whole, often expressed as a percentage. Understanding how to calculate these percentages is vital for creating accurate and informative charts. For example, if you're representing the market share of different companies, each company's share might be represented as a fraction or percentage of the whole pie chart.
-
Geometry and Trigonometry: In geometry, understanding fractions of circles is important for calculating areas of sectors and segments. A sector is a portion of a circle enclosed by two radii and an arc. A segment is the area enclosed by a chord and an arc.
-
Design and Engineering: Designers and engineers often use circles and their fractions in their work. For instance, in designing a circular clock face, understanding how to divide it into equal segments (representing hours or minutes) requires knowledge of fractions and percentages.
-
Everyday Life: Many situations involve dividing a whole into parts and expressing those parts as percentages. Consider sharing a pizza among friends; determining each person's share involves similar fraction and percentage calculations.
Expanding Your Understanding: Other Fractions of a Circle
Let's explore how to calculate percentages for other common fractions of a circle:
-
1/4 of a circle: 1 ÷ 4 = 0.25 => 0.25 × 100 = 25%
-
1/2 of a circle: 1 ÷ 2 = 0.5 => 0.5 × 100 = 50%
-
3/4 of a circle: 3 ÷ 4 = 0.75 => 0.75 × 100 = 75%
-
1/3 of a circle: 1 ÷ 3 ≈ 0.333 => 0.333 × 100 ≈ 33.33%
-
2/3 of a circle: 2 ÷ 3 ≈ 0.667 => 0.667 × 100 ≈ 66.67%
-
1/5 of a circle: 1 ÷ 5 = 0.2 => 0.2 × 100 = 20%
-
1/10 of a circle: 1 ÷ 10 = 0.1 => 0.1 × 100 = 10%
Working with More Complex Fractions
The principles remain the same even with more complex fractions. For example, to find the percentage represented by 5/8 of a circle:
-
Convert to Decimal: 5 ÷ 8 = 0.625
-
Convert to Percentage: 0.625 × 100 = 62.5%
Troubleshooting and Common Mistakes
When working with fractions and percentages of circles, it's important to avoid common mistakes:
-
Incorrect Division: Ensure you're dividing the numerator by the denominator correctly when converting the fraction to a decimal.
-
Incorrect Multiplication: Double-check your multiplication when converting the decimal to a percentage.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with fractions that result in repeating decimals. Use enough decimal places to ensure accuracy.
-
Misunderstanding the Concept: Make sure you have a firm grasp of the relationship between fractions, decimals, and percentages.
Conclusion: Mastering Circle Fractions and Percentages
Understanding how to calculate percentages of a circle is a valuable skill with wide-ranging applications. By grasping the fundamental concepts of fractions, decimals, and percentages, and by practicing the steps outlined in this guide, you can confidently tackle any problem involving fractions of a circle, from simple calculations to more complex scenarios in various fields. Remember to visualize the problem, check your work carefully, and don't hesitate to practice with various fractions to solidify your understanding. This knowledge will undoubtedly enhance your ability to interpret data, solve geometric problems, and excel in numerous other areas.
Latest Posts
Latest Posts
-
Evaluate The Trigonometric Function At The Quadrantal Angle
Apr 04, 2025
-
How Many Kilometers Is 11 Miles
Apr 04, 2025
-
170 Inches Is How Many Feet
Apr 04, 2025
-
Where In A Eukaryotic Cell Does Transcription Occur
Apr 04, 2025
-
Distance Covered Per Unit Of Time Is Called
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 1/8 Of A Circle Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
