X 3 3x 2 X 3 Factorise
Juapaving
May 12, 2025 · 5 min read
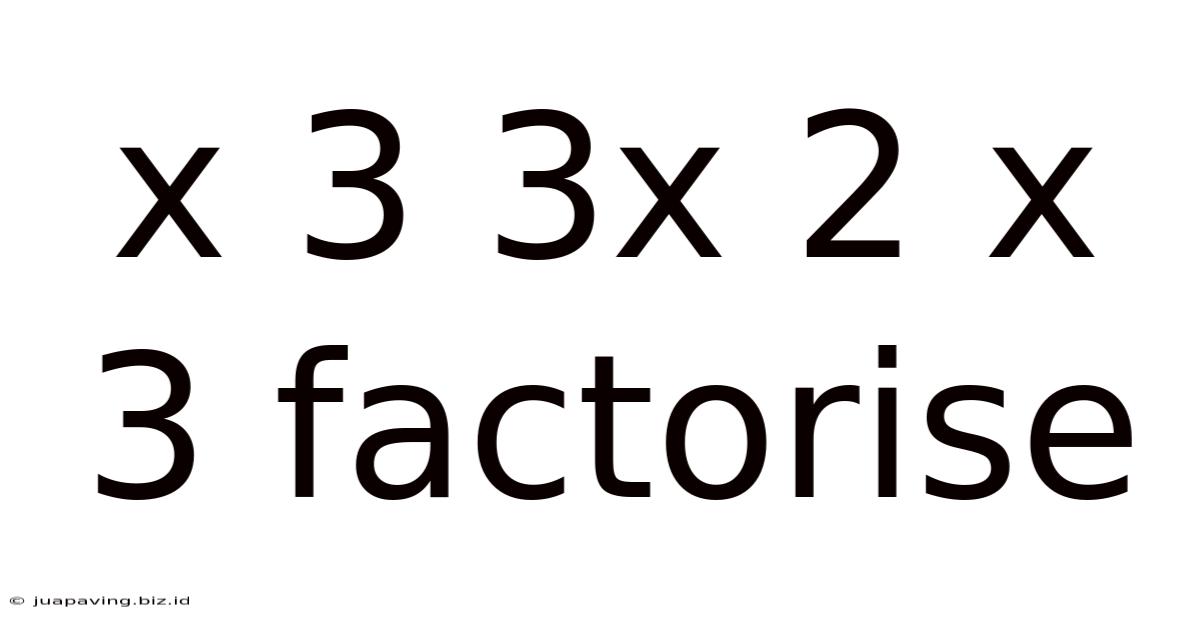
Table of Contents
Factorising Cubic Expressions: A Deep Dive into x³ + 3x² + 3x + 1
Factorising algebraic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding mathematical relationships. While linear and quadratic expressions are relatively straightforward to factorise, cubic expressions often present a greater challenge. This article delves into the factorisation of the specific cubic expression x³ + 3x² + 3x + 1, exploring various methods and providing a comprehensive understanding of the process. We'll examine the underlying mathematical principles and demonstrate how to approach similar problems effectively.
Understanding the Problem: x³ + 3x² + 3x + 1
Our target expression, x³ + 3x² + 3x + 1, represents a cubic polynomial. Factorisation involves expressing this polynomial as a product of simpler expressions, ideally linear factors. The process often involves identifying common factors, using special formulas, or employing techniques like grouping and polynomial long division.
Method 1: Recognizing the Pattern – The Binomial Expansion
This cubic expression is a perfect example of a binomial expansion. Recall the binomial theorem, which states:
(a + b)ⁿ = Σ (ⁿCᵣ) * aⁿ⁻ʳ * bʳ (where r goes from 0 to n)
For the case of (a + b)³, this expands to:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Comparing this expansion to our expression, x³ + 3x² + 3x + 1, we can see a clear resemblance:
- If we let a = x and b = 1, the expansion becomes: (x + 1)³ = x³ + 3x²(1) + 3x(1)² + 1³ = x³ + 3x² + 3x + 1
Therefore, the factorised form of x³ + 3x² + 3x + 1 is simply (x + 1)³.
This is the most elegant and efficient method for this specific cubic expression. Recognizing patterns and applying known formulas like the binomial theorem can significantly simplify the factorisation process.
Method 2: Rational Root Theorem and Polynomial Division
If the pattern wasn't immediately obvious, we could have used the Rational Root Theorem. This theorem helps identify potential rational roots (roots that are rational numbers) of a polynomial. The Rational Root Theorem states that any rational root p/q (where p and q are integers and q ≠ 0) of a polynomial must satisfy:
- p is a factor of the constant term (in our case, 1).
- q is a factor of the leading coefficient (in our case, 1).
Therefore, the possible rational roots of x³ + 3x² + 3x + 1 are ±1.
Let's test x = -1 using synthetic division or direct substitution:
- Direct Substitution: (-1)³ + 3(-1)² + 3(-1) + 1 = -1 + 3 - 3 + 1 = 0
Since substituting x = -1 results in 0, (x + 1) is a factor. Now, we perform polynomial long division to find the other factor:
x² + 2x + 1
_________________________
x + 1 | x³ + 3x² + 3x + 1
- (x³ + x²)
_________________
2x² + 3x
- (2x² + 2x)
_________________
x + 1
- (x + 1)
_________________
0
The result of the division is x² + 2x + 1. This quadratic expression can be further factorised as (x + 1)(x + 1).
Therefore, the complete factorisation is (x + 1)(x + 1)(x + 1) = (x + 1)³.
Method 3: Grouping (Less Effective in this Case)
The grouping method involves rearranging the terms and factoring out common factors from different groups. While less effective for this specific expression, it's a valuable technique for other cubic expressions. Attempting to group terms in x³ + 3x² + 3x + 1 doesn't yield a straightforward factorisation.
Expanding Our Understanding: General Cubic Factorisation
While the x³ + 3x² + 3x + 1 example showcases the binomial expansion and its efficiency, not all cubic expressions will follow such a neat pattern. Let's explore the broader context of cubic factorisation:
Cubic Equations and Their Roots
A cubic equation, of the form ax³ + bx² + cx + d = 0, will always have three roots (solutions). These roots can be real or complex numbers, and they may be repeated. Understanding the nature of these roots is key to factorisation.
Finding Roots: Numerical Methods
For more complex cubic expressions where direct factorisation isn't obvious, numerical methods are employed to approximate the roots. These methods include:
- Newton-Raphson Method: An iterative method that refines an initial guess to find a root.
- Bisection Method: A method that repeatedly halves an interval containing a root.
These methods are computationally intensive but provide accurate approximations when analytical solutions are unavailable.
The Importance of the Discriminant
The discriminant of a cubic equation helps determine the nature of its roots (real or complex, repeated or distinct). The cubic discriminant is a complex formula, but its value provides crucial information about the feasibility and approach to factorisation.
Applications of Cubic Factorisation
Factorising cubic expressions is crucial in numerous applications across various fields:
- Calculus: Finding critical points and inflection points of functions often involves solving cubic equations.
- Physics and Engineering: Many physical phenomena are modeled using cubic equations, requiring factorisation for analysis.
- Computer Graphics: Cubic curves (like Bézier curves) are extensively used in computer graphics, requiring factorisation for manipulation and analysis.
- Economics and Finance: Cubic models are used in economic forecasting and financial modeling, where factorisation plays a crucial role in analysis.
Conclusion: Mastering Cubic Factorisation
Factorising cubic expressions like x³ + 3x² + 3x + 1 is a valuable skill in mathematics and various related fields. Recognizing patterns and utilizing techniques such as the binomial expansion, the Rational Root Theorem, and polynomial division provides efficient strategies for finding factors. While more complex cubic expressions may necessitate numerical methods, a solid understanding of the fundamental techniques and the underlying principles empowers effective problem-solving. Remember to always check your factorisation by expanding the product of the factors to verify that it matches the original expression. Through practice and a thorough understanding of the concepts, mastering cubic factorisation becomes achievable, opening doors to more advanced mathematical concepts and applications.
Latest Posts
Latest Posts
-
How Many Meters Is 1 5 Km
May 12, 2025
-
Which Of The Following Is A Polar Molecule
May 12, 2025
-
How Many Cm In 5 5 Feet
May 12, 2025
-
What Is The Percent Of 0 4
May 12, 2025
-
An Animal Cell Placed In A Hypotonic Solution Will
May 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 X 3 Factorise . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.