X 3 3x 2 X 3
Juapaving
May 14, 2025 · 5 min read
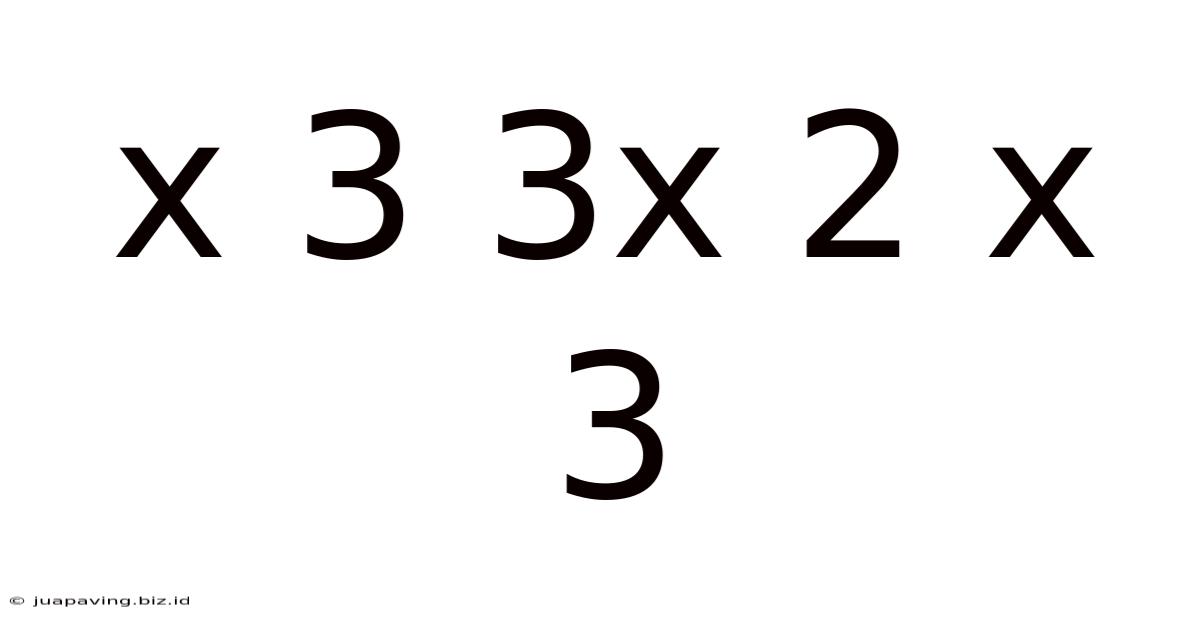
Table of Contents
Decoding the Mystery: A Deep Dive into x³ + 3x² + 3x + 1
The seemingly simple expression, x³ + 3x² + 3x + 1, holds a wealth of mathematical significance, far beyond its initial appearance. This article will explore this cubic polynomial in depth, examining its factorization, its connection to the binomial theorem, its graphical representation, and its applications in various fields. We’ll uncover why this seemingly innocuous expression is far more interesting than it initially seems.
Understanding the Polynomial's Structure
At first glance, x³ + 3x² + 3x + 1 appears to be a standard cubic polynomial. However, its coefficients – 1, 3, 3, and 1 – are strikingly familiar to anyone who has encountered the binomial theorem. These coefficients are, in fact, the binomial coefficients from the expansion of (a + b)³, where a = x and b = 1.
This connection is crucial to understanding the polynomial's most important characteristic: its perfect factorization.
Factorization: The Key to Understanding
The polynomial x³ + 3x² + 3x + 1 can be perfectly factored as (x + 1)³. This is directly derived from the binomial expansion:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Substituting a = x and b = 1, we get:
(x + 1)³ = x³ + 3x²(1) + 3x(1)² + 1³ = x³ + 3x² + 3x + 1
This simple factorization reveals a profound insight: the polynomial represents the cube of a binomial expression. This fundamental property underlies many of its applications.
The Binomial Theorem: A Deeper Connection
The binomial theorem, a cornerstone of algebra, provides a formula for expanding any binomial raised to a positive integer power. The general formula is:
(a + b)ⁿ = Σ (nCk) * aⁿ⁻ᵏ * bᵏ (where k ranges from 0 to n, and nCk represents the binomial coefficient "n choose k")
Our polynomial, x³ + 3x² + 3x + 1, is the specific case where n = 3, a = x, and b = 1. Understanding this connection allows us to generalize the concepts explored here to higher-order polynomials. For example, we can easily extend this to understand the expansion of (x+1)⁴, (x+1)⁵, and so on.
Graphical Representation and Root Analysis
Plotting the function y = x³ + 3x² + 3x + 1 reveals a simple cubic curve. Because it factors perfectly as (x+1)³, we can immediately identify its root. The only real root of this polynomial is x = -1. This is a root with multiplicity 3, meaning the graph touches the x-axis at x = -1 without crossing it. The graph is characterized by an inflection point at x = -1, where the curve changes concavity. The function continuously increases for all values of x, indicating a strictly monotonic function.
This graphical representation provides a visual confirmation of the polynomial's unique characteristics, reinforcing the mathematical analysis. The simplicity of the graph highlights the fundamental nature of the polynomial.
Applications in Various Fields
While seemingly abstract, this polynomial and its properties have several applications across diverse fields:
-
Calculus: Understanding its derivative and integral is straightforward due to its simple factored form. The derivative, 3(x+1)², helps in optimization problems, while the integral has applications in finding areas under curves.
-
Probability and Statistics: The binomial coefficients appearing in the polynomial are fundamental to probability calculations. They represent the probabilities of different outcomes in binomial distributions.
-
Physics and Engineering: Cubic equations frequently appear in physics and engineering problems, particularly those related to volume calculations, trajectory analysis, and the behavior of systems described by cubic relationships. Understanding the properties of this specific cubic polynomial might aid in simplifying or solving such equations.
-
Computer Science: Algorithms based on polynomial operations frequently involve simplifications akin to the factoring demonstrated here. Understanding such optimizations can improve algorithm efficiency.
-
Financial Modeling: Cubic polynomials can be utilized in financial modeling to represent various relationships between variables. The properties of this particular polynomial, due to its straightforward nature, can offer simplifications in such modeling efforts.
Extending the Concepts: Exploring Variations
We can modify the polynomial to explore related concepts:
-
Changing the constant term: Replacing the '1' with another constant would alter the factorization and the roots, leading to more complex analysis.
-
Varying the coefficients: Modifying the coefficients 1, 3, and 3 would change the polynomial's nature dramatically. It would no longer factor as a perfect cube.
-
Generalizing to higher powers: Extending the binomial theorem to higher powers (n > 3) leads to more complex polynomials with unique characteristics. Understanding this specific cubic case provides a solid foundation for exploring these more complex scenarios.
Further Exploration: Challenges and Opportunities
The polynomial x³ + 3x² + 3x + 1, despite its apparent simplicity, provides a rich ground for mathematical investigation. Further explorations could include:
-
Numerical analysis: Investigating numerical methods for finding roots, particularly for variations of the polynomial with less straightforward factorizations.
-
Complex roots: Exploring the behavior of modified versions of the polynomial which may exhibit complex roots.
-
Applications in other fields: Investigating potential applications in areas not explicitly mentioned above, such as cryptography or game theory.
Conclusion: The Significance of Simplicity
The expression x³ + 3x² + 3x + 1, while superficially simple, embodies fundamental mathematical concepts and provides a stepping stone to more complex analysis. Its straightforward factorization as (x+1)³ reveals a deep connection to the binomial theorem and offers valuable insights into the nature of cubic polynomials. The exploration of this polynomial demonstrates the beauty and power of mathematical simplification, highlighting how seemingly simple expressions can hold vast and profound implications. Understanding this specific case provides a strong foundation for tackling more intricate mathematical problems and exploring their applications in numerous fields. The simplicity of its structure belies the wealth of information it contains, serving as a potent reminder of the elegance and power of mathematical principles.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about X 3 3x 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.