X 3 2x 2 5x 10
Juapaving
May 10, 2025 · 5 min read
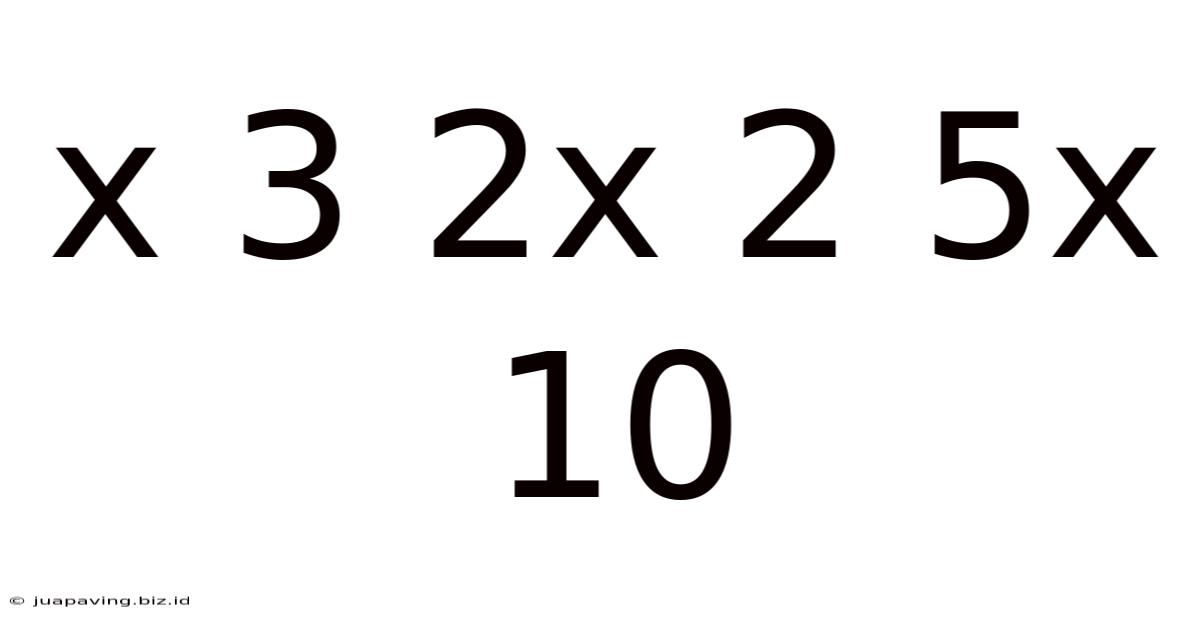
Table of Contents
Decoding the Mathematical Expression: x³ + 2x² + 5x + 10
This article delves deep into the mathematical expression x³ + 2x² + 5x + 10, exploring its various aspects, from basic understanding to advanced applications. We will uncover its properties, potential solutions, and how it relates to broader mathematical concepts. This comprehensive guide is designed to be accessible to a wide audience, from students grappling with polynomial expressions to those interested in exploring more advanced mathematical principles.
Understanding the Basics: Polynomial Expressions
Before we dive into the specifics of x³ + 2x² + 5x + 10, let's establish a foundational understanding of polynomial expressions. A polynomial is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. In our case, we have a polynomial in a single variable, x.
Key Components of a Polynomial:
- Terms: Each part of the polynomial separated by a plus or minus sign is a term. Our expression has four terms: x³, 2x², 5x, and 10.
- Coefficients: The numerical factors multiplying the variables are called coefficients. In our polynomial, the coefficients are 1 (for x³), 2 (for 2x²), 5 (for 5x), and 10 (for the constant term).
- Variables: These are the symbols representing unknown values (in our case, x).
- Exponents: The powers to which the variables are raised are called exponents. The exponents in our polynomial are 3, 2, 1 (implied for 5x), and 0 (for the constant term 10, since x⁰ = 1).
- Degree: The highest exponent of the variable in a polynomial is its degree. Our polynomial is a cubic polynomial (degree 3) because the highest exponent of x is 3.
Types of Polynomials Based on Degree:
- Constant Polynomial: Degree 0 (e.g., 5)
- Linear Polynomial: Degree 1 (e.g., 2x + 3)
- Quadratic Polynomial: Degree 2 (e.g., x² + 4x - 7)
- Cubic Polynomial: Degree 3 (e.g., our expression x³ + 2x² + 5x + 10)
- Quartic Polynomial: Degree 4 (e.g., x⁴ - 2x³ + x² - 5x + 1)
- and so on...
Factoring the Polynomial: Unveiling Hidden Structures
Factoring a polynomial means expressing it as a product of simpler polynomials. This process is crucial for solving equations, simplifying expressions, and gaining insights into the polynomial's behavior. Let's try to factor x³ + 2x² + 5x + 10.
We can use a technique called factoring by grouping. This method involves grouping terms with common factors:
(x³ + 2x²) + (5x + 10)
Now we factor out the common factors from each group:
x²(x + 2) + 5(x + 2)
Notice that both terms now share a common factor of (x + 2). We can factor this out:
(x + 2)(x² + 5)
Therefore, the factored form of x³ + 2x² + 5x + 10 is (x + 2)(x² + 5). This factorization reveals the polynomial's structure more clearly.
Understanding the Factored Form:
The factored form tells us that the polynomial will equal zero when either (x + 2) = 0 or (x² + 5) = 0.
- (x + 2) = 0: This gives us a real root of x = -2.
- (x² + 5) = 0: This gives us two complex roots: x = ±√(-5) = ±i√5, where 'i' is the imaginary unit (√-1).
Graphical Representation and Behavior
Plotting the polynomial x³ + 2x² + 5x + 10 on a graph provides visual insights into its behavior. The graph will be a curve that rises from the left to the right, crossing the x-axis at x = -2 (the real root). The imaginary roots don't appear on the real x-y plane. The curve's shape is characteristic of a cubic polynomial.
Applications of Cubic Polynomials
Cubic polynomials, like our example, have diverse applications in various fields:
- Engineering: Modeling the trajectory of projectiles, designing curves for roads and bridges, and analyzing the behavior of mechanical systems.
- Physics: Describing the motion of objects under the influence of forces, and modeling wave phenomena.
- Economics: Analyzing economic growth models and forecasting trends.
- Computer Graphics: Creating smooth curves and surfaces in computer-aided design (CAD) and computer-generated imagery (CGI).
- Chemistry: Modeling chemical reactions and rates of reaction.
Solving Cubic Equations: Methods and Techniques
Solving a cubic equation, such as setting our polynomial equal to zero (x³ + 2x² + 5x + 10 = 0), involves finding the values of x that satisfy the equation. Several methods can be employed:
- Factoring: As demonstrated earlier, factoring is the most straightforward method if the polynomial can be factored easily.
- Rational Root Theorem: This theorem helps identify potential rational roots (roots that are fractions).
- Numerical Methods: For cubic equations that are difficult or impossible to factor, numerical methods like the Newton-Raphson method provide approximate solutions.
- Cardano's Method: A more advanced algebraic method for solving cubic equations.
Advanced Concepts and Extensions
The analysis of x³ + 2x² + 5x + 10 can be extended to more advanced concepts:
- Partial Fraction Decomposition: This technique is used to decompose rational functions (fractions of polynomials) into simpler fractions.
- Taylor and Maclaurin Series: These series represent functions as infinite sums of polynomials, allowing for approximations and analysis of function behavior.
- Calculus: The derivative and integral of our cubic polynomial can be calculated to understand its rate of change and area under the curve.
Conclusion: A Deeper Appreciation of Polynomials
This comprehensive exploration of x³ + 2x² + 5x + 10 has revealed the multifaceted nature of polynomial expressions. From basic understanding of terms and coefficients to advanced factorization techniques and applications, we've uncovered the richness and depth of this seemingly simple mathematical expression. This exploration underscores the importance of polynomials in diverse scientific and engineering fields, highlighting their significance in modeling real-world phenomena and solving complex problems. Further exploration into the related fields of algebra, calculus, and numerical analysis will reveal even more profound insights into the power and versatility of polynomial functions. Remember that continued learning and practice are essential for mastering these concepts and applying them effectively.
Latest Posts
Latest Posts
-
What Is The End Product Starch Digestion
May 10, 2025
-
What Fraction Is Equivalent To 18 75
May 10, 2025
-
Male And Female Pelvis Differences Table
May 10, 2025
-
Where Does Gas Exchange Take Place In Plants
May 10, 2025
-
How Does Increasing Volume Affect Equilibrium
May 10, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 5x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.