Write The Prime Factorization Of 54
Juapaving
Apr 01, 2025 · 5 min read
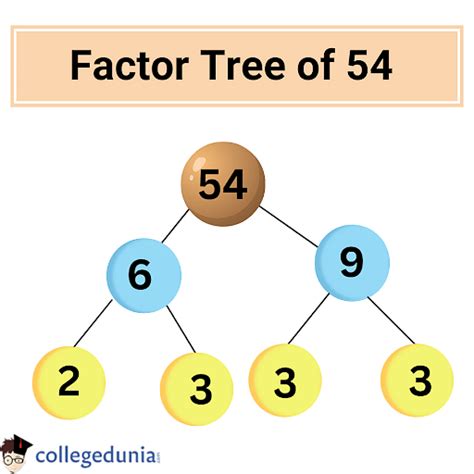
Table of Contents
Unveiling the Prime Factorization of 54: A Deep Dive into Number Theory
The seemingly simple question, "What is the prime factorization of 54?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, understanding the process and the underlying concepts provides a solid foundation for tackling more complex mathematical problems. This article will not only provide the prime factorization of 54 but will also explore the broader significance of prime numbers and factorization in mathematics and its applications.
Understanding Prime Numbers
Before we delve into the factorization of 54, let's establish a clear understanding of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
Prime numbers are the fundamental building blocks of all other numbers. This fundamental property is the cornerstone of number theory and has significant implications across various fields, including cryptography and computer science.
Distinguishing Prime Numbers from Composite Numbers
It's crucial to differentiate between prime numbers and composite numbers. A composite number is a positive integer greater than 1 that is not prime; that is, it has at least one divisor other than 1 and itself. For example, 4, 6, 9, and 12 are composite numbers. Every composite number can be expressed as a unique product of prime numbers, a concept known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factorization of 54
Now, let's address the main question: What is the prime factorization of 54? Prime factorization is the process of expressing a composite number as a product of its prime factors. We can achieve this through a systematic approach:
-
Start with the smallest prime number, 2. Is 54 divisible by 2? Yes, 54 divided by 2 is 27.
-
Move to the next prime number, 3. Is 27 divisible by 2? No. Is it divisible by 3? Yes, 27 divided by 3 is 9.
-
Continue with the next prime number, 3 again. Is 9 divisible by 3? Yes, 9 divided by 3 is 3.
-
We've reached another prime number, 3. Is 3 divisible by 3? Yes, 3 divided by 3 is 1.
We've reached 1, indicating that we've completed the factorization. Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3, which can also be written as 2 x 3³.
Visualizing the Factorization Process: Factor Tree
A factor tree provides a visual representation of the factorization process. Here's how a factor tree would look for 54:
54
/ \
2 27
/ \
3 9
/ \
3 3
The prime factors at the end of the branches are 2, 3, 3, and 3. This confirms our earlier calculation.
The Significance of Prime Factorization
The seemingly simple act of finding the prime factorization of a number holds far-reaching implications in various mathematical fields and applications:
1. Fundamental Theorem of Arithmetic: Uniqueness
The prime factorization of any composite number is unique (disregarding the order of the factors). This is a cornerstone of number theory, guaranteeing a consistent and predictable way to represent any composite number. This uniqueness enables many advanced mathematical operations and proofs.
2. Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Streamlining Calculations
Prime factorization simplifies the calculation of the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers. By using prime factorization, these calculations become significantly easier and more efficient.
For instance, let's find the GCD and LCM of 54 and 72.
First, find their prime factorizations:
- 54 = 2 x 3³
- 72 = 2³ x 3²
To find the GCD, we take the lowest power of each common prime factor: GCD(54, 72) = 2¹ x 3² = 18
To find the LCM, we take the highest power of each prime factor present in either number: LCM(54, 72) = 2³ x 3³ = 216
3. Cryptography: Securing Digital Information
Prime numbers play a crucial role in modern cryptography. Many encryption algorithms, such as RSA (Rivest-Shamir-Adleman), rely on the difficulty of factoring very large composite numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring such numbers, protecting sensitive data transmitted over the internet. The larger the prime numbers used, the more secure the encryption becomes.
4. Modular Arithmetic: A Foundation for Computer Science
Prime factorization and modular arithmetic are closely related. Modular arithmetic involves performing arithmetic operations within a specific range (a modulus). Prime numbers have unique properties within modular arithmetic, making them essential in various computer science applications, including hash functions and error-correcting codes.
5. Number Theory Research: Expanding Mathematical Knowledge
Prime factorization continues to be a subject of active research in number theory. Questions surrounding the distribution of prime numbers, the efficiency of factorization algorithms, and the properties of prime numbers remain areas of ongoing exploration, driving advancements in mathematical understanding.
Beyond 54: Exploring Further
The prime factorization of 54 serves as a springboard for understanding broader concepts in number theory. By mastering the techniques involved in finding prime factorizations, you can tackle increasingly complex mathematical problems. The ability to efficiently factor numbers is not just an academic exercise; it's a fundamental skill with real-world applications in cryptography, computer science, and various other fields. Exploring different factoring methods, such as trial division and the Pollard Rho algorithm (for larger numbers), will further enhance your mathematical capabilities.
Conclusion: The Enduring Importance of Prime Factorization
The seemingly simple act of finding the prime factorization of 54 offers a gateway to a vast and fascinating world of mathematical exploration. Understanding prime numbers and prime factorization is crucial not only for solving mathematical problems but also for comprehending the underlying principles that govern many aspects of modern technology and cryptography. The knowledge gained from understanding this fundamental concept extends far beyond the realm of mathematics, impacting various fields and driving continuous advancements in our understanding of numbers and their properties. So, while the answer to "What is the prime factorization of 54?" might seem simple (2 x 3³), the journey to understanding it unlocks a deeper appreciation of the elegance and power of mathematics.
Latest Posts
Latest Posts
-
What Tpye Of Reacgion Is Word Bank
Apr 02, 2025
-
How Many Feet Is 103 Inches
Apr 02, 2025
-
What Is The Difference Between A Niche And A Habitat
Apr 02, 2025
-
What Is 30 Percent Of 120
Apr 02, 2025
-
Difference Between Violet And Purple Color
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Write The Prime Factorization Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
